Introduksjon til hierarkisk gruppering algoritme
Den hierarkiske grupperingsalgoritmen er en maskinlæringsteknikk uten tilsyn. Den tar sikte på å finne naturlig gruppering basert på egenskapene til dataene.
Den hierarkiske grupperingsalgoritmen tar sikte på å finne nestede grupper av dataene ved å bygge hierarkiet. Det ligner på den biologiske taksonomien til plante- eller dyreriket. Hierarkiske klynger er generelt representert ved å bruke det hierarkiske treet kjent som et dendrogram.
Typer hierarkisk gruppering algoritme
Hierarkiske grupperingsalgoritmer er av to typer:
- splittende
- agglomerative
1. Delende
Dette er en ovenfra og ned-tilnærming, der den i utgangspunktet betrakter hele dataene som en gruppe, og deretter iterativt deler opp dataene i undergrupper. Hvis tallet på en hierarkisk klynge-algoritme er kjent, stopper delingsprosessen når antall klynger er oppnådd. Ellers stopper prosessen når dataene ikke kan deles mer, noe som betyr at undergruppen hentet fra den nåværende iterasjonen er den samme som den som ble oppnådd fra forrige iterasjon (man kan også vurdere at divisjonen stopper når hvert datapunkt er en klynge ).
2. Agglomerativ
Det er en bottom-up tilnærming som er avhengig av sammenslåing av klynger. Opprinnelig blir dataene delt opp i m singleton-klynger (hvor verdien av m er antall prøver / datapunkter). To klynger er slått sammen til en iterativt, og dermed reduserer antall klynger i hver iterasjon. Denne prosessen med å slå sammen klynger stopper når alle klynger er blitt slått sammen til ett eller antall oppnådde klynger oppnås.
På nivå 1 er det m klynger som blir redusert til 1 klynge på nivå m. De datapunktene som blir slått sammen for å danne en klynge på et lavere nivå, holder seg også i samme klynge på de høyere nivåene. Antar at det er 8 punkter x1..x8, så til å begynne med er det 8 klynger på nivå 1. Anta at punktene x1 og x2 blir slått sammen til en klynge på nivå 2, så til nivå 8, de forblir i samme klynge.
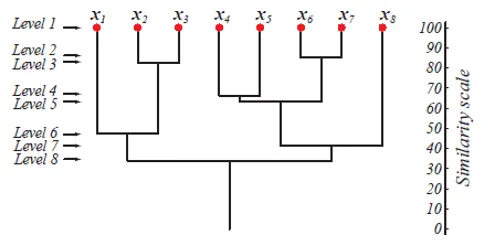
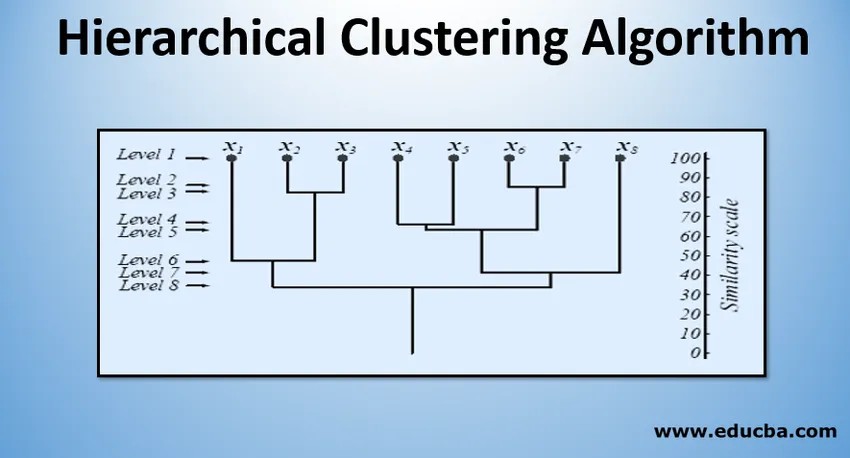
Figuren ovenfor viser en dendrogram-representasjon av tilnærmingen til agglomereringsklynger for 8 datapunkter samt likhetsskalaen som tilsvarer hvert nivå.
Nivåene på klynger gir oss en ide om hvor like datapunktene i klyngene er. Som vist på fig. 1, blir datapunktene tidligere slått sammen til en klynge, de samme er de. Så datapunktene i en klynge på nivå 2 (f.eks. X2 og x3) er mer like enn datapunktene i en klynge på nivå 6 (f.eks. X1 og x2).
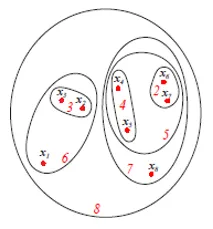
Figuren over viser Set- eller Venn-diagram-representasjonen av den agglomerative klyngebeningen til de ovennevnte 8 datapunkter. Både dendrograms og setrepresentasjoner kan brukes til gruppering. Imidlertid er et dendrogram vanligvis foretrukket formuesrepresentasjon kan ikke kvantitativt representere klyngens likheter.
Trinn for hierarkisk gruppering algoritme
La oss følge følgende trinn for den hierarkiske klynge-algoritmen som er gitt nedenfor:
1. Algoritme
Agglomerativ hierarkisk grupperingsalgoritme
- Begynn å initialisere c, c1 = n, Di = (xi), i = 1, …, n '
- Gjør c1 = c1 - 1
- Finn nærmeste klynger, si Di og Dj
- Slå sammen Di og Dj
- Inntil c = c1
- Returner klynger
- Slutt
Denne algoritmen begynner med n klynger opprinnelig der hvert datapunkt er en klynge. Med hver iterasjon reduseres antall klynger med 1 når de 2 nærmeste klyngene blir slått sammen. Denne prosessen fortsetter til antall klynger reduseres til den forhåndsdefinerte verdien c.
Hvordan bestemme hvilke klynger som er i nærheten?
Dette er definert ved å bruke flere avstandsmålinger som er som følger:
- Minste avstand mellom klyngene dmin (Di, Dj). Nyttig for singel.
- Maksimal avstand mellom klyngene dmax (Di, Dj). Nyttig for fullstendig.
- Den gjennomsnittlige avstanden mellom klyngene davg (Di, Dj).
Hva er enkeltkobling og fullstendig kobling?
- Når dmin (di, dj) brukes til å finne avstanden mellom to klynger, og algoritmen avsluttes hvis avstanden mellom de nærmeste klyngene overstiger en terskel, kalles algoritmen en enkelt koblingsalgoritme.
- Når dmax (Di, Dj) brukes til å finne avstanden mellom to klynger, og algoritmen avsluttes hvis avstanden mellom de nærmeste klyngene overstiger en terskel, kalles algoritmen en komplett koblingsalgoritme.
- La oss betrakte hvert datapunkt som en node på en graf. Det er en kant mellom to datapunkter hvis de tilhører samme klynge. Når to nærmeste klynger er slått sammen, legges en kant til. Det kalles en enkelt kobling fordi det eksisterer en unik bane fra den ene noden til den andre.
- Den komplette koblingsalgoritmen fusjonerer to klynger ved å minimere avstanden mellom de to fjerneste punktene.
- En enkelt koblingsalgoritme genererer et spenntre. Imidlertid er denne algoritmen utsatt for støy. En komplett koblingsalgoritme genererer en fullstendig graf.
Hva er tidskompleksiteten til algoritmen?
Anta at vi har n mønstre i d-dimensjonalt rom, og vi bruker dmin (Di, Dj) til å danne c klynger. Vi må beregne n (n - 1) mellompunktavstander - som hver er en O (d 2 ) beregning - og plassere resultatene i en avstandstabell mellom punkter. Romkompleksiteten er O (n 2 ). Å finne minimumsavstandparet (for den første sammenslåingen) krever at vi går gjennom den komplette listen og holder indeksen for den minste avstanden.
For det første agglomerative trinnet er kompleksiteten således O (n (n - 1) (d2 + 1)) = O (n 2 d2). For et annet vilkårlig agglomerasjonstrinn (dvs. fra c1 til c1 - 1), går vi bare gjennom n (n - 1) - c1 "ubrukte" avstander i listen og finner de minste som x og x 'ligger i forskjellige klynger . Dette er igjen O (n (n − 1) −c1). Den totale tidskompleksiteten er således O (cn 2 d 2 ), og under typiske forhold er n >> c.
2. Visualisering
Når dataene er delt opp i klynger, er det en god praksis å visualisere klyngene for å få et inntrykk av hvordan ser grupperingene ut. Men å visualisere disse høydimensjonale dataene er vanskelig. Derfor bruker vi Principal Component Analysis (PCA) for visualisering. Etter PCA oppnår vi datapunktene i det lave dimensjonsområdet (vanligvis 2D eller 3D) som vi kan plotte for å se gruppering.
Merk: Høy dimensjon betyr et stort antall funksjoner og ikke et antall datapunkter.3. Evaluering
En av metodene for evaluering av klynger er at avstanden til punktene mellom klyngene (avstand mellom klynger) skal være mye mer enn avstanden til punktene innenfor klyngen (intracluster avstand).
Konklusjon
Følgende er noen viktige takeaways:
- Den hierarkiske grupperingsalgoritmen brukes til å finne nestede mønstre i data
- Hierarkisk klynging er av to typer - Delende og agglomerativ
- Dendrogram og sett / Venn-diagram kan brukes til representasjon
- Enkeltkobling slår sammen to klynger ved å minimere minimumsavstanden mellom dem. Det danner et spenn
- Komplett kobling fusjonerer to klynger ved å minimere den maksimale avstanden mellom Det danner en komplett graf.
- Den totale tidskompleksiteten til hierarkisk grupperingsalgoritme er O (cn 2 d 2 ), hvor c er det forhåndsdefinerte antall klynger, n er antall mønstre og d er det d-dimensjonale rommet til n mønstrene.
Anbefalte artikler
Dette er en guide til Hierarkisk Clustering-algoritmen. Her diskuterer vi typene og trinnene for hierarkiske grupperingsalgoritmer. Du kan også se på følgende artikler for å lære mer-
- Hierarkisk Clustering Analyse
- Hierarkisk klynge i R '
- Clustering algoritme
- Hva er Clustering i datamining?
- Hierarkisk klynging | Agglomerative & Divisive Clustering
- C ++ algoritme | Eksempler på C ++ algoritme