Forskjellen mellom lineær regresjon vs logistisk regresjon
Følgende artikkel Linear Regression vs Logistic Regression gir de viktigste forskjellene mellom begge, men før vi får se hva betyr Regresjon?
regresjon
Regresjon er i utgangspunktet et statistisk mål for å bestemme styrken i forholdet mellom en avhengig variabel, dvs. utgangen Y og en serie andre uavhengige variabler, dvs. X 1, X 2 og så videre. Regresjonsanalyse brukes i utgangspunktet til prediksjon og prognoser.
Hva er lineær regresjon?
Lineær regresjon er en algoritme som er basert på det veiledede læringsdomenet til maskinlæring. Det arver et lineært forhold mellom inngangsvariablene og den enkle utgangsvariabelen der utgangsvariabelen er kontinuerlig. Det brukes til å forutsi verdien av output, la oss si Y fra inngangene, la oss si X. Når bare en enkelt inngang blir vurdert, kalles det enkel lineær regresjon.
Det kan klassifiseres i to hovedkategorier:
1. Enkel regresjon
Operasjonsprinsipp: Hovedmålet er å finne ut ligningen på en rett linje som best passer samplede data. Denne ligningen beskriver algebraisk forholdet mellom de to variablene. Den best passende linjen kalles regresjonslinje.
Y = β 0 + β 1 X
Hvor,
β representerer funksjonene
β 0 representerer avskjæringen
ß 1 representerer koeffisienten for funksjon X
2. Multivariabel regresjon
Det brukes til å forutsi en sammenheng mellom mer enn en uavhengig variabel og en avhengig variabel. Regresjon med mer enn to uavhengige variabler er basert på passende form til konstellasjonen av data på en flerdimensjonal graf. Regresjonsformen skal være slik at den minimerer avstanden til formen fra hvert datapunkt.
En lineær relasjonsmodell kan fremstilles matematisk som nedenfor:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Hvor,
β representerer funksjonene
β 0 representerer avskjæringen
β 1 representerer koeffisienten for funksjon X1
β n representerer koeffisienten for funksjon Xn
Fordeler og ulemper ved lineær regresjon
Nedenfor er fordeler og ulemper:
Fordeler
- På grunn av sin enkelhet blir den mye brukt modellering for spådommer og konklusjoner.
- Det fokuserer på dataanalyse og dataforbehandling. Så, den tar for seg forskjellige data uten å bry seg om detaljene i modellen.
ulemper
- Det fungerer effektivt når dataene normalt distribueres. For effektiv modellering må således kollineariteten unngås.
Hva er logistisk regresjon?
Det er en form for regresjon som tillater prediksjon av diskrete variabler ved en blanding av kontinuerlige og diskrete prediktorer. Det resulterer i en unik transformasjon av avhengige variabler som påvirker ikke bare estimeringsprosessen, men også koeffisientene til uavhengige variabler. Den tar opp det samme spørsmålet som flere regresjoner gjør, men uten fordelingsmessige forutsetninger for prediktorene. I logistisk regresjon er utfallsvariabelen binær. Hensikten med analysen er å vurdere effekten av flere forklaringsvariabler, som kan være numeriske eller kategoriske eller begge deler.
Typer logistisk regresjon
Nedenfor er de to typene logistisk regresjon:
1. Binær logistisk regresjon
Den brukes når den avhengige variabelen er dikotom, dvs. som et tre med to grener. Den brukes når den avhengige variabelen er ikke-parametrisk.
Brukes når
- Hvis det ikke er linearitet
- Det er bare to nivåer av den avhengige variabelen.
- Hvis multivariat normalitet er tvilsomt.
2. Multinomial logistisk regresjon
Multinomial logistisk regresjonsanalyse krever at de uavhengige variablene er metriske eller dikotomme. Den legger ikke til grunn antagelser om linearitet, normalitet og homogenitet av varians for de uavhengige variablene.
Den brukes når den avhengige variabelen har mer enn to kategorier. Den brukes til å analysere sammenhenger mellom en ikke-metrisk avhengig variabel og metriske eller dikotome uavhengige variabler, for deretter å sammenligne flere grupper gjennom en kombinasjon av binære logistiske regresjoner. Til slutt gir det et sett med koeffisienter for hver av de to sammenligningene. Koeffisientene for referansegruppen er alle nuller. Til slutt gjøres prediksjon basert på den høyeste resulterende sannsynligheten.
Fordel med logistisk regresjon: Det er en veldig effektiv og mye brukt teknikk siden den ikke krever mange beregningsressurser og ikke krever noen innstilling.
Ulempen med logistisk regresjon: Den kan ikke brukes til å løse ikke-lineære problemer.
Head to Head sammenligning mellom Lineær Regresjon vs Logistisk Regresjon (Infografikk)
Nedenfor er de topp 6 forskjellene mellom Lineær regresjon vs logistisk regresjon 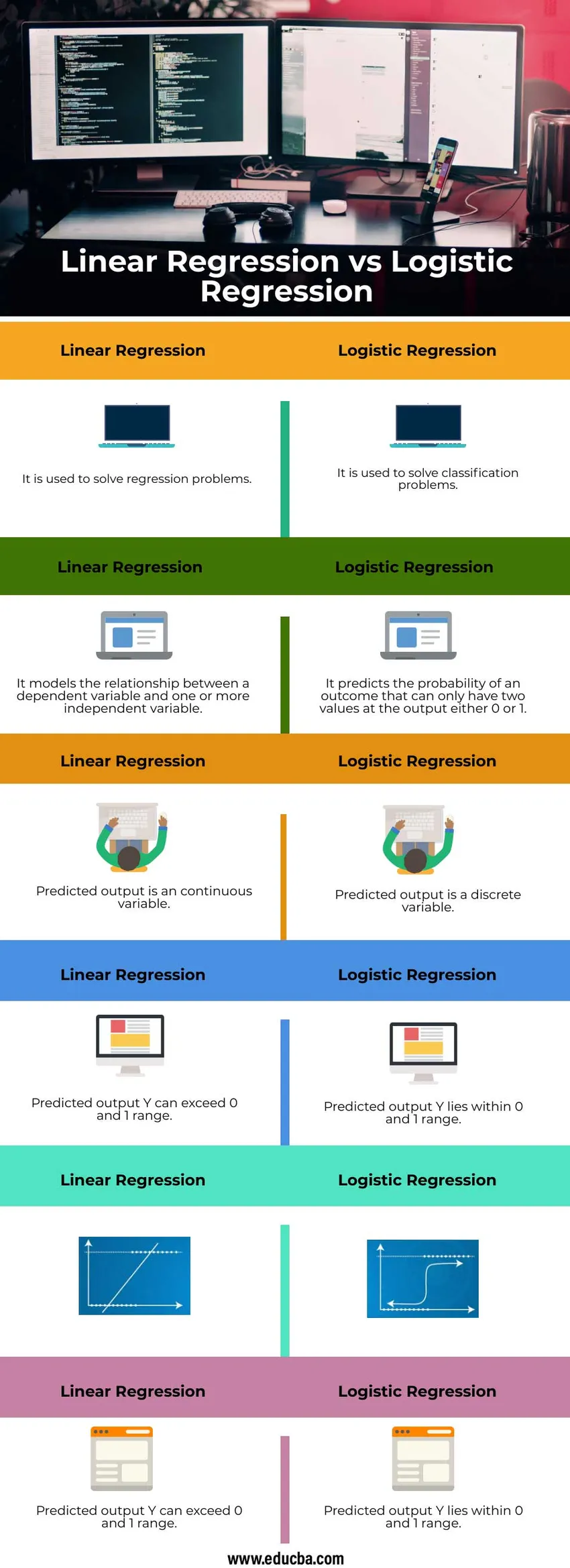
Nøkkelforskjellen mellom den lineære regresjonen vs logistisk regresjonen
La oss diskutere noen av de viktigste nøkkelforskjellene mellom Lineær Regresjon vs Logistisk Regresjon
Lineær regresjon
- Det er en lineær tilnærming
- Den bruker en rett linje
- Det kan ikke ta kategoriske variabler
- Det må ignorere observasjoner med manglende verdier av den numeriske uavhengige variabelen
- Utgang Y er gitt som
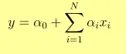
- 1 enhetsøkning i x øker Y med α
applikasjoner
- Å forutsi prisen på et produkt
- Å spå poengsum i en kamp
Logistisk regresjon
- Det er en statistisk tilnærming
- Den bruker en sigmoid-funksjon
- Det kan ta kategoriske variabler
- Den kan ta beslutninger selv om observasjoner med manglende verdier er til stede
- Utgang Y er gitt som, der z er gitt som
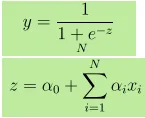
- 1 enhetsøkning i x øker Y ved loggodds på α
- Hvis P er sannsynligheten for en hendelse, er (1-P) sannsynligheten for at den ikke skal skje. Odds for suksess = P / 1-P
applikasjoner
- Å spå om det i dag vil regne eller ikke.
- Å spå om en e-post er spam eller ikke.
Tabell for sammenligning av lineær regresjon vs logistisk regresjon
La oss diskutere toppsammenligningen mellom Lineær regresjon vs logistisk regresjon
|
Lineær regresjon |
Logistisk regresjon |
| Det brukes til å løse regresjonsproblemer | Det brukes til å løse klassifiseringsproblemer |
| Den modellerer forholdet mellom en avhengig variabel og en eller flere uavhengige variabler | Den spår sannsynligheten for et utfall som bare kan ha to verdier ved utgangen, enten 0 eller 1 |
| Det predikerte resultatet er en kontinuerlig variabel | Den predikerte utgangen er en diskret variabel |
| Forutsatt utgang Y kan overstige 0 og 1 område | Forutsatt utgang Y ligger innenfor 0 og 1 område |
 | 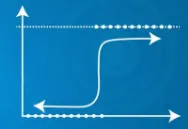 |
| Forutsatt utgang Y kan overstige 0 og 1 område | Forutsatt utgang |
Konklusjon
Hvis funksjoner ikke bidrar til prediksjon, eller hvis de er veldig korrelert med hverandre, så gir det støy til modellen. Så funksjoner som ikke bidrar nok til modellen, må fjernes. Hvis uavhengige variabler er sterkt korrelert, kan det føre til et problem med multikollinearitet, som kan løses ved å kjøre separate modeller med hver uavhengige variabel.
Anbefalte artikler
Dette har vært en guide til Linear Regression vs Logistic Regression. Her diskuterer vi Linear Regression vs Logistic Regression viktige forskjeller med infografikk og sammenligningstabell. Du kan også se på følgende artikler for å lære mer–
- Data Science vs Data Visualization
- Machine Learning vs Neural Network
- Veiledet læring vs dyp læring
- Logistisk regresjon i R