
Introduksjon til Firkanter i Java
Når et tall multipliseres med seg selv, er det resulterende tallet som dannes, kvadratet for tallet. Ruter med et antall er veldig enkle å finne. Generelt sett når vi finner kvadratroten til et heltall, får vi bare resultatet i heltall. Tilsvarende får vi svaret i desimal når vi finner kvadratet med et desimaltall. Et interessant faktum med kvadratet til et tall er at når vi gjør en kvadrat med et heltall, øker verdien av det resulterende tallet. Imidlertid, når vi gjør kvadratet med desimaler mellom 0 og 1, reduseres det resulterende antallet. Et eksempel er en kvadrat på 0, 5. Når vi kvadraterer 0, 5, blir antallet redusert til 0, 25. I denne artikkelen skal vi se de forskjellige metodene for hvordan vi kan kvadratere et tall ved å bruke programmeringsspråket Java.
Working - Square med et antall kan bli funnet på Java ved en rekke teknikker. Vi vil gjerne se noen eksempler relatert til kvadratet til et tall som vi kan forstå kvadratet til et tall bedre.
Hvordan beregner jeg Square i Java?
La oss lære å beregne kvadrat i java:
Eksempel 1
Den enkleste måten å finne kvadratet til et tall er Math.pow () der det kan brukes til å beregne hvilken som helst effekt på et tall.
Kode:
import java.util.*;
public class Square
(
public static void main(String args())
(
Scanner sc=new Scanner(System.in);
int num;
System.out.print("Enter a number which is integer format: ");
num=sc.nextInt();
System.out.println("The square of "+ num + " is: "+ Math.pow(num, 2));
)
)
Produksjon:

Eksempel 2
I neste program skal vi beregne kvadratet til et tall i vanlig form slik at det multipliserer to tall i rekkefølge og finner kvadratet til det respektive tallet.
Kode:
import java.util.*;
public class Square2
(
public static void main(String args())
(
Scanner sc=new Scanner(System.in);
int no;
System.out.print("Enter a number which is integer format: ");
no=sc.nextInt();
System.out.println("Square of "+ no + " is: "+(no*no));//the number is multiplied with its own
)
)
Produksjon:

Eksempel 3
I dette eksemplet skal vi sjekke om et tall er et perfekt torg eller ikke. Dette er et lite sammensatt program da det sjekker om et tall er et kvadrat med et annet tall.
Kode:
import java.util.Scanner;
class JavaExample (
static boolean checkPerfectSquare(double x)
(
// finding the square root of given number
double s= Math.sqrt(x);
return ((s - Math.floor(s)) == 0); //Math.floor() is used here to calculate the lower value.
)
public static void main(String() args)
(
System.out.print("Enter any number:");
Scanner scanner = new Scanner(System.in);
double no= scanner.nextDouble();
scanner.close();
if (checkPerfectSquare(no))
System.out.print(no+ " is a perfect square number");
else
System.out.print(no+ " is not a perfect square number");
)
)
Produksjon:

Eksempel 4
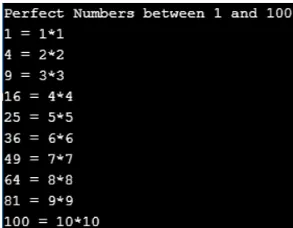
I dette programmet finner vi antall firkantede tall innenfor et spesifikt område. Vi legger inn tallområdet og koden produserer kvadratnummeret i det spesifikke området. I programmet nedenfor finner vi antall firkantede tall mellom 0 og 100.
Kode:
// Finding the range of perfect square numbers in Java programming language
import java.io.IOException;
public class SquareNumbersInRange (
public static void main(String() args) throws IOException (
int starting_number = 1;
int ending_number = 100;
System.out.println("Perfect Numbers between "+starting_number+ " and "+ending_number);
for (int i = starting_number; i <= ending_number; i++) (
int number = i;
int sqrt = (int) Math.sqrt(number);
if (sqrt * sqrt == number) (
System.out.println(number+ " = "+sqrt+"*"+sqrt);
)
)
)
)
Produksjon:
Eksempel 5
I dette programmet skal vi se summen av kvadratene med de første N naturlige tallene. Vi legger inn verdien på N og programmet beregner summen av kvadrater for de første N naturlige tallene.
Kode:
// Java Program to find sum of
// square of first n natural numbers
import java.io.*;
class SumofSquares
(
// Return the sum of the square of first n natural numbers
static int square sum(int n)
(
// Move the loop of I from 1 to n
// Finding square and then adding it to 1
int sum = 0;
for (int i = 1; i <= n; i++)
sum += (i * i);
return sum;
)
// Main() used to print the value of sum of squares
public static void main(String args()) throws IOException
(
int n = 6;
System.out.println("The sum of squares where N value is 6 is "+ squaresum(n));
)
)
Produksjon:

Konklusjon
- I denne artikkelen ser vi en liste over metoder som vi kan kvadratere et tall, hvordan vi kan finne ut om et tall er kvadratisk eller ikke innenfor et spesifikt område, og også summen av heltal for de første N naturlige tallene. Imidlertid er det også noen andre teknikker som kan brukes til å finne kvadratet til et tall. Navnet på en teknikk som kan brukes til å se og sjekke om et tall er kvadrat eller ikke, er rekursjonsteknikken som bruker en funksjon i en funksjon for å sjekke om tallet er et perfekt kvadrat eller ikke.
- Selv om rekursjonsteknikken er vanskelig å bruke, kan den brukes til å beregne kvadratet til et tall i løpet av noen få kodelinjer. Ved å bruke firkantede tall kan vi dessuten generere mange mønsterprogrammer. Vi kan trykke et firkantet mønster i spiralformat eller i et sikksakk-format. Tilsvarende kan firkantetallene brukes i kildekoden for å generere det doble kvadratet, for eksempel tallet 16 der det doble kvadratet er nummer 2.
Anbefalte artikler
Dette er en guide til rutene i Java. Her har vi diskutert introduksjonen langs eksempler og koder med Output of Squares i Java. Du kan også gå gjennom de andre foreslåtte artiklene våre for å lære mer–
- Mønstre i Java
- Cheat Sheet JavaScript
- Hva er webapplikasjon?
- Typer webhotell
- Square Root i PHP
- Arrays i Java-programmering
- Working and Top 3 Enum Methods in C #
- Square Root i JavaScript