Introduksjon til hierarkisk klynging
- Nylig ba en av våre kunder teamet vårt om å få frem en liste over segmenter med en rekkefølge av betydning i kundene sine for å målrette dem om å franchise et av deres nylig lanserte produkter. Det er klart at bare segmentering av kundene ved bruk av delvis klynging (k-betyr, c-fuzzy) ikke vil få frem rekkefølgen av viktighet som er der hierarkisk klynging kommer inn i bildet.
- Hierarkisk klynging er å dele dataene i forskjellige grupper basert på noen likhetstiltak kjent som klynger, som i hovedsak har som mål å bygge hierarkiet mellom klynger. Det er i utgangspunktet uovervåket læring og å velge attributter for å måle likhet er applikasjonsspesifikk.
Klyngen av datahierarki
- Agglomerative Clustering
- Delende klynger
La oss ta et eksempel på data, karakterer oppnådd av 5 elever for å gruppere dem til en kommende konkurranse.
| Student | Marks |
| EN | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Agglomerative Clustering
- Til å begynne med vurderer vi hvert enkelt punkt / element her vekt som klynger og fortsetter å slå sammen de samme punktene / elementene for å danne en ny klynge på det nye nivået til vi sitter igjen med den ene klyngen er en bottom-up tilnærming.
- Enkeltkobling og fullstendig kobling er to populære eksempler på agglomerativ gruppering. Annet enn den gjennomsnittlige koblingen og Centroid-koblingen. I enkeltkobling slår vi sammen i hvert trinn de to klyngene, hvis to nærmeste medlemmer har den minste avstanden. I fullstendig kobling fletter vi sammen medlemmene på den minste avstanden som gir den minste maksimale parvise avstanden.
- Nærhetsmatrise, det er kjernen for å utføre hierarkisk klynging, som gir avstanden mellom hvert av punktene.
- La oss lage nærhetsmatrise for dataene våre som er gitt i tabellen, siden vi beregner avstanden mellom hvert av punktene med andre punkter vil det være en asymmetrisk matrise med form n × n, i vårt tilfelle 5 × 5 matriser.
En populær metode for avstandsberegning er:
- Euklidisk avstand (kvadrat)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattan-avstand
dist((x, y), (a, b)) =|x−c|+|y−d|
Euklidisk avstand er mest brukt, vi vil bruke den samme her, og vi vil gå med kompleks kobling.
| Student (Clusters) | EN | B | C | D | E |
| EN | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 1. 3 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 1. 3 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonale elementer i nærhetsmatrise vil alltid være 0, ettersom avstanden mellom punktet med det samme punktet alltid vil være 0, og dermed er diagonale elementer unntatt fra hensynet til gruppering.
Her, i iterasjon 1, er den minste avstanden 3, og dermed fletter vi A og B for å danne en klynge, danner igjen en ny nærhetsmatrise med klyngen (A, B) ved å ta (A, B) klyngepunktet som 10, dvs. maksimalt ( 7, 10) så nylig dannet nærhetsmatrise ville være
| klynger | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
I iterasjon 2, 7 er den minste avstanden. Derfor fletter vi C og E og danner en ny klynge (C, E), vi gjentar prosessen som følges i iterasjon 1 til vi ender opp med den ene klyngen, her stopper vi ved iterasjon 4.
Hele prosessen er avbildet i figuren nedenfor:
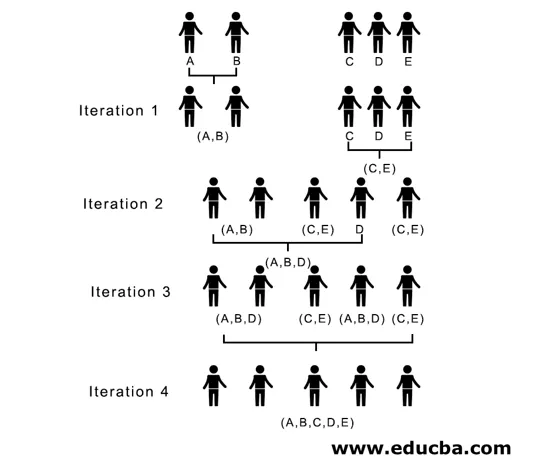
(A, B, D) og (D, E) er de to klyngene som er dannet ved iterasjon 3, ved den siste iterasjonen kan vi se at vi sitter igjen med en enkelt klynge.
2. Delende klynger
Til å begynne med anser vi alle punkter som en enkelt klynge og skiller dem med den fjerneste avstanden til vi slutter med individuelle punkter som individuelle klynger (ikke nødvendigvis kan vi stoppe i midten, avhenger av minimum antall elementer vi ønsker i hver klynge) på hvert trinn. Det er bare det motsatte av agglomerativ klynging, og det er en ovenfra og ned-tilnærming. Delende klynger er en måte repeterende k betyr klynging på.
Å velge mellom Agglomerative og Divisive Clustering er igjen applikasjonsavhengig, men få punkter som må vurderes er:
- Delende er mer sammensatt enn agglomerativ klynging.
- Delende klynger er mer effektive hvis vi ikke genererer et komplett hierarki ned til individuelle datapunkter.
- Agglomerativ klyngering tar en beslutning ved å vurdere de lokale klapperne, uten å ta hensyn til globale mønstre i utgangspunktet som ikke kan reverseres.
Visualisering av hierarkisk klynging
En super nyttig metode for å visualisere hierarkisk klynging som hjelper i virksomheten er Dendogram. Dendogrammer er trelignende strukturer som registrerer sekvensen av sammenslåinger og splitter der vertikal linje representerer avstanden mellom klyngene, avstanden mellom vertikale linjer og avstanden mellom klyngene er direkte proporsjonal, dvs. mer avstanden mer klyngene vil sannsynligvis være ulik.
Vi kan bruke dendogrammet til å bestemme antall klynger, bare tegne en linje som skjærer hverandre med en lengste vertikale linje på dendogrammet, et antall vertikale linjer som krysses, vil være antall klynger som skal vurderes.
Nedenfor er eksemplet Dendogram.
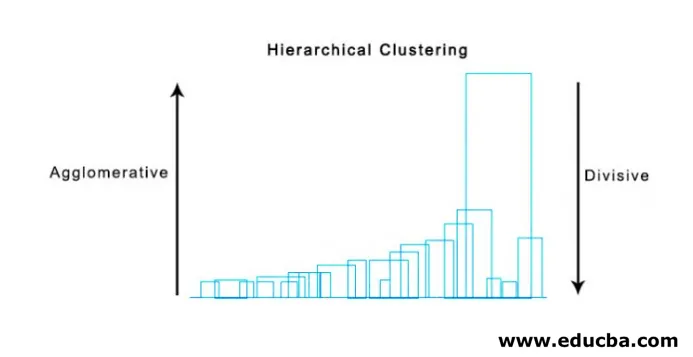
Det er ganske enkle og direkte pythonpakker, og det er funksjoner for å utføre hierarkisk gruppering og plottendendogrammer.
- Hierarkiet fra scipy.
- Cluster.hierarchy.dendogram for visualisering.
Vanlige scenarier der hierarkisk klynging brukes
- Kundesegmentering til markedsføring av produkter eller tjenester.
- Byplanlegging for å identifisere stedene å bygge strukturer / tjenester / bygning.
- Sosialt nettverk analyse, for eksempel identifisere alle MS Dhoni fans for å annonsere hans biopic.
Fordeler med hierarkisk klynging
Fordelene er gitt nedenfor:
- Når det gjelder delvis klynging som k-middel, bør antall klynger være kjent før klynging, noe som ikke er mulig i praktiske anvendelser, mens det i hierarkisk klynging ikke er nødvendig med forkunnskaper om antall klynger.
- Hierarkisk klynging gir et hierarki, dvs. en mer informativ struktur enn det ustrukturerte settet med flate klynger som er returnert ved delvis klynging.
- Hierarkisk klynging er enkel å implementere.
- Viser resultater i de fleste scenarier.
Konklusjon
Type klynging utgjør den store forskjellen når data blir presentert, og hierarkisk klynging er mer informativ og enkel å analysere er mer foretrukket enn delvis klynging. Og det er ofte forbundet med varmekart. For ikke å glemme attributter som er valgt for å beregne likhet eller ulikhet, hovedsakelig påvirker både klynger og hierarki.
Anbefalte artikler
Dette er en guide til hierarkisk klynging. Her diskuterer vi introduksjonen, fordelene ved Hierarkisk Clustering og Common Scenarios der Hierarchical Clustering brukes. Du kan også gå gjennom de andre foreslåtte artiklene våre for å lære mer–
- Clustering algoritme
- Clustering in Machine Learning
- Hierarkisk klynge i R
- Clustering Methods
- Hvordan fjerne hierarki i Tableau?