
Excel SIN-funksjon (innholdsfortegnelse)
- SIN-funksjon i Excel
- Hvordan bruker du SIN-funksjon i Excel?
SIN-funksjon i Excel
Å kunne beregne omfatter ikke matematikkens helhet. Det er en del av den, om enn viktig i bruken. I årene som gikk var det den begrensende faktoren, bortsett fra de mye anerkjente og ekstremt talentfulle 'menneskelige kalkulatorene', som Shakuntala Devi. Men datamaskiner lar deg nå gjøre hele matematikken mer intellektuell. Begrepene og teoriene i matematikk er mer fremtredende nå enn noen gang før.
Excel er veldig flink til å håndtere en mengde matematiske modeller, er bevæpnet med en enorm samling av matematiske og logiske funksjoner for å støtte forskjellige operasjoner. Den gir en hel serie trigonometriske funksjoner som kan hjelpe oss når vi går inn i trigonometriens verden.
Så for å løse den trigonometriske funksjonen Sine, gir den SIN-funksjonen . Det er en grunnleggende trigonometrisk funksjon, men kommer godt med, spesielt hvis du jobber med industri, navigasjon eller kommunikasjonsindustri. Men det er viktig å merke seg at Excel bruker radianer, ikke grader for å beregne noe trigonometrisk uttrykk. Det er to måter å gjøre dette på:
- Husk at π = 180 °. Så hvis vinkelen er i grader, multipliser den med π / 180 ° for å konvertere den til radianer. I Excel kan denne konverteringen skrives PI () / 180. For å konvertere 60 ° til radianer, vil Excel-uttrykket for eksempel være 60 * PI () / 180, som tilsvarer 1.0472 radianer.
- Excel er også utstyrt med et veldig nyttig verktøy ofte referert til som RADIANS. Den aksepterer en vinkel som et argument, der vinkelen refererer til de grader som må transformeres til radianer. Ta forekomsten der uttrykket som brukes til å transformere 210 ° til radianer er "RADIANS (210)", og det vurderes til 66519 radianer.
Motsatt er DEGREES-verktøyet like viktig. Denne funksjonen kan brukes til å gjøre det motsatte av RADIANS-funksjonen, ved å konvertere radianer til grader. Som et eksempel evaluerer DEGREES (PI () / 2) 90.
Hvordan bruker du SIN-funksjon i Excel?
La oss forstå hvordan du bruker SIN-funksjon i Excel ved å bruke noen eksempler og virkelige illustrasjoner av SIN-funksjon i Excel.
Du kan laste ned denne SIN-funksjonen Excel-malen her - SIN-funksjonen Excel-malenSIN-funksjon i Excel - eksempel # 1
Beregne sinusverdi ved å bruke SIN-funksjon i Excel
For å finne sinusen til et bestemt tall, må vi først skrive = SIN () i en bestemt celle.

Som du kan se fra skjermbildet ovenfor, forventer SIN-funksjonen i Excel et nummer som inndata. Dette tallet representerer vanligvis en verdi i radianer.
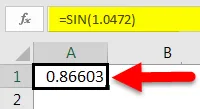
Så i dette tilfellet vil vi skrive “= SIN (1.0472)”, der 1.0472 er radianene som tilsvarer 60 grader.
Når vi har gjort dette, vil vi få SIN-verdien på 60 grader.
SIN-funksjon i Excel - eksempel # 2
Beregne sinusverdi ved å bruke SIN og RADIAN-funksjon i Excel
La oss nå se hvordan vi kan bruke SIN på en mer produktiv måte, i tilfelle når vi ikke vet den eksakte radianverdien for en grad.
Vi vil bruke RADIANS () for å finne ut radianverdien, som vi vil gi som et argument til SIN-funksjonen.
Så begynner vi med den tidligere versjonen av SIN ():

Neste, vil vi sende RADIANS (60) som et argument til SIN-funksjonen, der 60 er verdien i grader.

Som vi ser av eksemplet over, godtar RADIANS () en verdi i grader. Så vi skal passere 60 som verdien til RADIANS ().

Trykk deretter Enter. Dette gir følgende resultat.

Så vi ser at resultatet er det samme som det første eksemplet.
SIN-funksjon i Excel - eksempel # 3
Beregne sinusverdi ved å bruke SIN og PI-funksjon i Excel
Det er enda en måte å konvertere en gradverdi til radianer til å bruke i SIN-funksjonen. Vi husker fra vår tid på skolen at π = 180 °. Så hvis vinkelen er i grader, multipliser den med π / 180 ° for å konvertere den til radianer. I Excel kan denne konverteringen skrives PI () / 180. For å konvertere 60 ° til radianer, vil Excel-uttrykket for eksempel være 60 * PI () / 180, som tilsvarer 1.0472 radianer.
La oss se hvordan dette fungerer:
Vi begynner med å skrive SIN-funksjonen på samme måte som ovenfor.

Neste, vil vi direkte passere 60 ° som argumentet til SIN-funksjonen. Men dette ville ikke gi oss den tilsvarende verdien på 60 grader i radianer. Derfor vil vi multiplisere 60 med PI () / 180.

Dette vil gi oss følgende resultat:
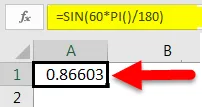
Som vi ser er dette det samme som eksemplene ovenfor.
SIN-funksjon i Excel - eksempel # 4
La oss se på et annet eksempel som viser resultatene av SIN-funksjonen for forskjellige verdier.

Forklaring av resultatene vist i tabellen over:
Sak 1 og 2:
3.14 er verdien av Pi, og vi kan bruke begge metodene for å få en verdi av 0. Dette betyr i utgangspunktet at SIN for Pi-radianer er 0 .
Sak 3 og 4:
Radianer og Pi / 180 har lik verdi i matematikk og derav gir SIN-funksjon samme verdi. Begge eksempler antyder SIN på 30 grader som gir en verdi på 0, 5.
Sak 5 og 6:
SIN 45 = 0, 85 er SIN på 45 radianer som betyr at excel som standard tar alle vinklene i radianer og ikke grad. For å konvertere den til grad kan vi bruke radian-funksjon og få SIN på 45 grader som vist i siste rad. dvs. SIN (RADIANS (45)) = 0, 707 eller 0, 71
SIN-funksjon i Excel - eksempel # 5
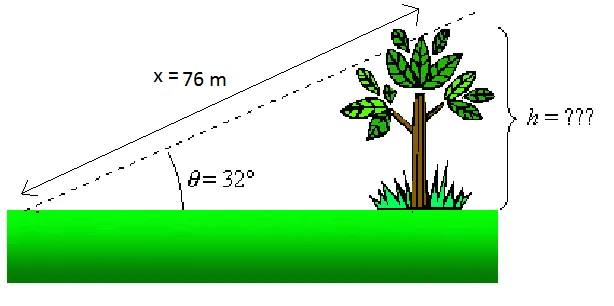
Si for eksempel at vi vil vite høyden på treet i figuren vist over. Vi vet at hvis vi står 76 m fra toppen av treet (x = 76 m), er siktlinjen til toppen av treet 32 ° i forhold til horisonten (θ = 32 °). Vi vet det:
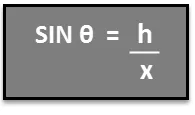
Derfor for å løse for høyden på treet h, finner vi h = x SIN θ.

SIN-funksjonen har bare ett argument som er et tall. Det kreves et nummer for å beregne SIN av den. Derfor er det viktig å konvertere grader til et antall i radianer før du finner Sine av det.
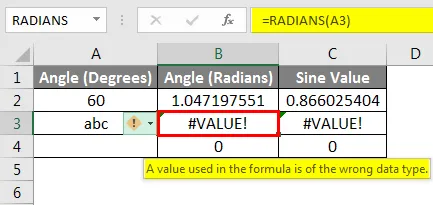
SIN-funksjonen viser #VALUE! feil hvis referansen som brukes som funksjonens argument peker til en celle som inneholder tekstdata. I eksemplet vist nedenfor peker cellereferansen til den tredje raden som brukes til tekstetiketten i Vinkel (grader) . Siden SIN-funksjonene bare støtter et nummer som et argument, vil SIN evaluere til en feil, i dette tilfellet #VALUE! . Hvis cellen peker til en tom celle, returnerer funksjonen en verdi på null som vist i eksemplet nedenfor. Excel's trigonometriske funksjoner tolker blanke celler som null, og sinusen til null radianer er lik null.
SIN-funksjon i Excel - eksempel # 6
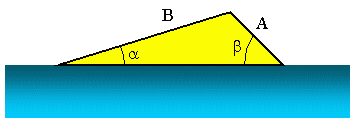
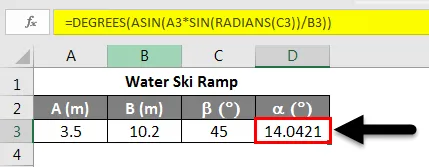
Anta at vi ønsker å finne ut lanseringsvinkelen til en vannski rampe som på figuren over. Vi vet at A = 3, 5 m, B = 10, 2 m og b = 45, 0 °. Nå for å finne en, kan vi bruke loven om sines. I dette scenariet kan det skrives som:
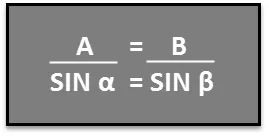
Vi kan organisere denne ligningen på nytt som:
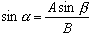
Ved bruk av bueskinn eller invers sinus kan vi finne ut vinkelen α . Bruk av ligningen vist nedenfor.

Eksempel 7
I vårt endelige trigonometriske eksempel vil vi bruke Excel til å undersøke den trigonometriske identiteten:
sin²θ + cos²θ = 1
Merk at i skjermdumpen nedenfor stemmer denne identiteten når when er gitt i både radianer og grader.

Legg merke til at enhetsbeskrivelsen for vinkelen θ er plassert i forskjellige celler enn tallene. Hvis vi plasserer tallene og enhetene i samme celle, vil Excel ikke kunne skille tallet fra teksten, og vi vil derfor ikke kunne referere til cellene som skal brukes i en ligning, og det vil resultere i #VALUE! feil.
Ting å huske
- Husk at SIN-funksjonen i Excel fungerer med Radian som standard.
- Konverter antall etter behov i Radian eller Degree ved å bruke enten RADIANS-funksjon eller DEGREES-funksjon.
- Du kan bruke PI () -funksjonen for å få eksakte resultater av SIN-funksjonen mens du arbeider med π.
Anbefalte artikler
Dette har vært en guide til SIN-funksjon i Excel. Her diskuterte vi Hvordan bruke SIN-funksjon i Excel sammen med praktiske eksempler og nedlastbar Excel-mal. Du kan også gå gjennom andre foreslåtte artikler -
- Viktige funksjoner i matematikk i Excel (enkelt)
- Veiledning for deling av formler i Excel
- Viktige avanserte Excel-formler og funksjoner
- Jukseark med Excel-formler