
Introduksjon til DFS-algoritme
DFS er kjent som Dybden første søkealgoritme som gir trinnene for å krysse hver eneste node i en graf uten å gjenta noen node. Denne algoritmen er den samme som Depth First Traversal for et tre, men skiller seg i å opprettholde en boolsk for å sjekke om noden allerede er besøkt eller ikke. Dette er viktig for grafovergang, da det også finnes sykluser i grafen. En stabel opprettholdes i denne algoritmen for å lagre de suspenderte nodene mens de går. Det heter det fordi vi først reiser til dybden til hver tilstøtende node og deretter fortsetter å krysse en annen tilstøtende node.
Forklar DFS-algoritmen
Denne algoritmen er i strid med BFS-algoritmen der alle tilstøtende noder blir besøkt fulgt av naboer til de tilstøtende noder. Den begynner å utforske grafen fra en node og utforsker dens dybde før backtracking. To ting blir vurdert i denne algoritmen:
- Besøk i en toppunkt: Valg av en toppunkt eller knute av grafen for å krysse.
- Utforsking av en toppunkt: Krysser alle nodene ved siden av det toppunktet.
Pseudokode for dybde Første søk :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Linear Traversal eksisterer også for DFS som kan implementeres på tre måter:
- Forhåndsbestille
- I rekkefølge
- Postorder
Omvendt postorder er en veldig nyttig måte å krysse av og brukes i topologisk sortering samt forskjellige analyser. En stabel opprettholdes også for å lagre nodene hvis utforskning fremdeles er i påvente.
Graph Traverse i DFS
I DFS følges trinnene nedenfor for å krysse grafen. For eksempel, en gitt graf, la oss starte traversering fra 1:
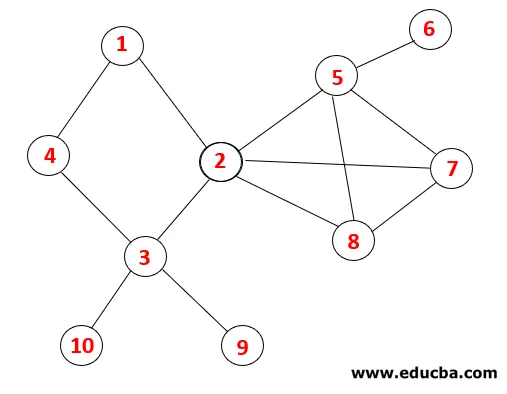
| Stable | Traversal Sequence | Spanning Tree |
| 1 |  |
|
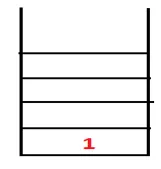 | 1, 4 |  |
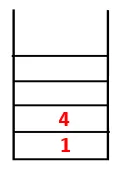 | 1, 4, 3 |  |
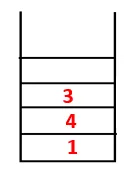 | 1, 4, 3, 10 | 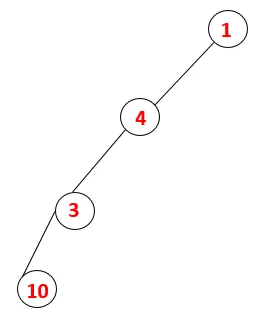 |
 | 1, 4, 3, 10, 9 | 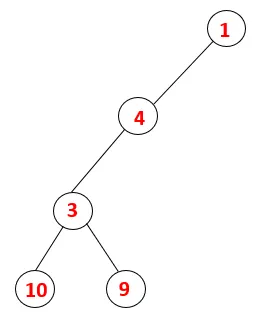 |
 | 1, 4, 3, 10, 9, 2 | 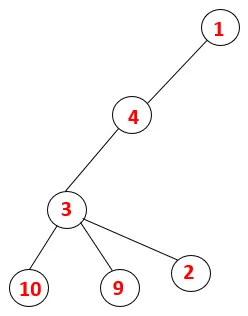 |
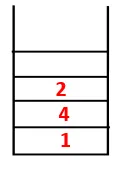 | 1, 4, 3, 10, 9, 2, 8 |  |
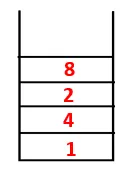 | 1, 4, 3, 10, 9, 2, 8, 7 | 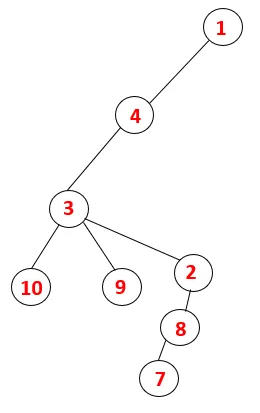 |
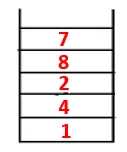 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
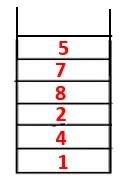 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 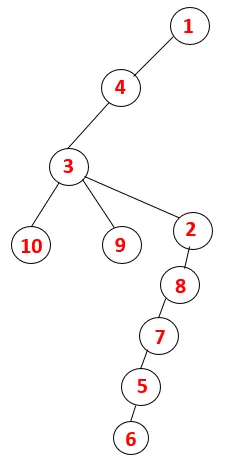 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 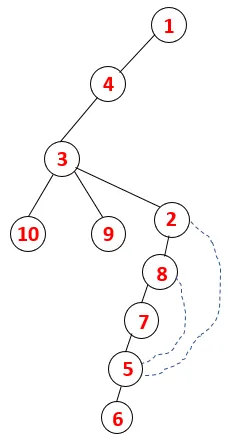 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
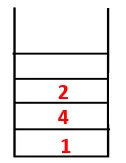 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 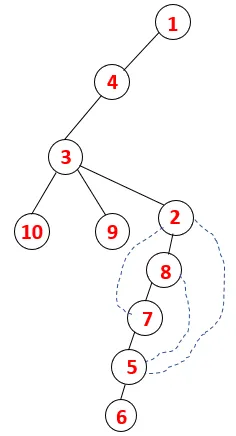 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 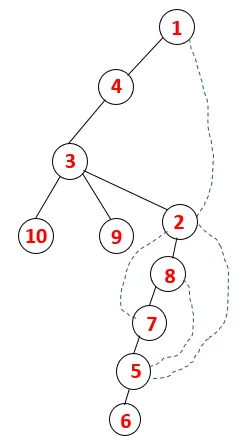 |
Forklaring til DFS-algoritme
Nedenfor er trinnene til DFS Algoritme med fordeler og ulemper:
Trinn 1: Node 1 besøkes og legges til i sekvensen, så vel som det spanderende treet.
Trinn 2: Tilstøtende noder av 1 blir utforsket som er 4, slik at 1 skyves til bunken og 4 skyves inn i sekvensen så vel som spanningstreet.
Trinn 3: En av de tilstøtende nodene til 4 blir utforsket og dermed 4 skyvet til stabelen, og 3 går inn i sekvensen og det spant treet.
Trinn 4: Tilstøtende noder av 3 blir utforsket ved å skyve den på stabelen og 10 går inn i sekvensen. Ettersom det ikke er noen tilstøtende knutepunkt til 10, blir 3 således slått ut av stabelen.
Trinn 5: En annen tilstøtende node av 3 blir utforsket og 3 dyttet inn på stabelen og 9 blir besøkt. Ingen tilstøtende knutepunkt på 9 og dermed 3 blir plukket ut, og den siste tilstøtende knutepunkt på 3 dvs. 2 blir besøkt.
Tilsvarende prosess følges for alle noder til bunken blir tom, noe som indikerer stopptilstanden for kryssingsalgoritmen. - -> stiplede linjer i treet som refererer til bakkantene i grafen.
På denne måten går alle nodene i grafen gjennom uten å gjenta noen av nodene.
Fordeler og ulemper
- Fordeler: Dette minnekravet for denne algoritmen er veldig mindre. Mindre rom og tidskompleksitet enn BFS.
- Ulemper: Løsning er ikke garantert Programmer. Topologisk sortering. Finne grafer.
Eksempel på implementering av DFS-algoritme
Nedenfor er eksemplet for implementering av DFS-algoritme:
Kode:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Produksjon:
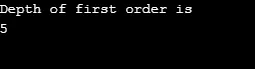
Forklaring til ovennevnte program: Vi laget en graf med 5 vertikaler (0, 1, 2, 3, 4) og brukte besøkt matrise for å holde oversikt over alle besøkte toppunkt. Deretter gjentas for hver node med tilstøtende noder samme algoritme til alle nodene blir besøkt. Deretter går algoritmen tilbake til å ringe toppunkt og sprette den fra bunken.
Konklusjon
Minnekravet til denne grafen er mindre sammenlignet med BFS ettersom det bare er behov for å opprettholde en stabel. Et DFS som spenner over tre og traversalsekvens genereres som et resultat, men er ikke konstant. Flere traversalsekvenser er mulig avhengig av valgt toppunkt og letekode.
Anbefalte artikler
Dette er en guide til DFS Algoritme. Her diskuterer vi trinnvis forklaring, krysse grafen i et tabellformat med fordeler og ulemper. Du kan også gå gjennom andre relaterte artikler for å lære mer -
- Hva er HDFS?
- Deep Learning Algorithms
- HDFS-kommandoer
- SHA-algoritme