Introduksjon til matematikkfunksjoner i C ++
Det er vanskelig og tidkrevende når du må skrive kode hver gang for å gjøre grunnleggende matematiske beregninger i programmet. Derfor gir C ++ et stort antall mattefunksjoner for å gjøre koden din enkel og effektiv. Du kan utføre et stort antall operasjoner på tall ved hjelp av mattefunksjoner. Siden disse funksjonene er innebygd og støttet av biblioteket i C ++, så er det nødvendig å ta med overskriftsfil eller i begynnelsen av koden for å bruke alle funksjonalitetene i mattefunksjoner. Du trenger ikke å skrive logikkoden i koden for å utføre operasjoner. Det hele er der i biblioteket.
Ulike typer matematikkfunksjoner
C ++ gir et stort antall forskjellige typer mattefunksjoner nevnt nedenfor med eksempler:
1. Maksimal og minimum funksjon
- maks (p, q): Det vil returnere et maksimaltall mellom p og q.
- min (p, q): Det vil returnere et minimumstall mellom p og q.
C ++ -kode for å implementere over funksjonalitet
#include
#include
using namespace std;
int main() (
cout << max(16, 18) << "\n";
cout << min(16, 18) << "\n";
return 0;
)
Produksjon:

2. Kraftfunksjoner
- pow (m, n): Det vil beregne m hevet til kraften n.
- kvm (m): Det vil beregne kvadratroten til m.
- cbrt (n): Det vil beregne kubusroten til n.
- hypot (m, n): Det vil beregne hypotenusen til den rettvinklede trekanten.
C ++ kode for å implementere funksjonalitet ovenfor
#include
#include
using namespace std;
int main() (
cout << pow(2, 3) << "\n";
cout << sqrt(16) << "\n";
cout << cbrt(27) << "\n";
cout << hypot(3, 4) << "\n";
return 0;
)
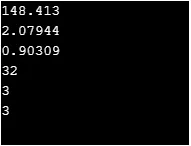
Produksjon:

3. Eksponentielle funksjoner
- exp (p): Den vil beregne den eksponentielle e hevet til makten p.
- log (p): Den vil beregne logaritmen til p.
- log10 (p): Den vil beregne den vanlige logaritmen til p.
- exp2 (p): Det vil beregne eksponentiell base 2 for p.
- log2 (p): Den vil beregne basis 2-logaritmen til p.
- logb (p): Den vil beregne logaritmen til p.
C ++ kode for å implementere funksjonalitet ovenfor
#include
#include
using namespace std;
int main() (
cout << exp(5) << "\n";
cout << log(8) << "\n";
cout << log10(8) << "\n";
cout << exp2(5) << "\n";
cout << log2(8) << "\n";
cout << logb(8) << "\n";
return 0;
)
Produksjon:
4. Heltallsfunksjoner
Det hjelper med å finne den nærmeste heltallverdien.
- tak (z): det avrunder verdien av z.
- etasje (z): det avrunder verdien av z.
- runde (z): Det avrunder verdien av z.
- fmod (z, y): Den beregner resten av divisjon z / y.
- trunc (z): Den vil avrunde z-verdien mot null.
- rint (z): Det avrunder z-verdien ved bruk av avrundingsmodus.
- nearbyint (z): Det avrunder z-verdien til en integrert verdi i nærheten.
- resten (z, y): Den vil beregne resten av z / y.
C ++ kode for å implementere funksjonalitet ovenfor
#include
#include
using namespace std;
int main() (
cout << ceil(4580.01) << "\n";
cout << floor(151.999) << "\n";
cout << round(518.5) << "\n";
cout << fmod(5, 21) << "\n";
cout << trunc(20.25) << "\n";
cout << rint(21.25) << "\n";
cout << nearbyint(182.55) << "\n";
cout << remainder(12, 36) << "\n";
return 0;
)
Produksjon:
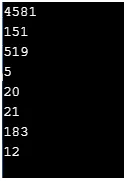
5. Sammenligningsfunksjoner
Hjelp til å sammenligne tall i et raskt spenn spiller ingen rolle hvor lenge tallet er. Nedenfor er noen eksempler på sammenligningsfunksjoner:
- isgreater (p, q): Den sjekker om p er større enn q eller ikke.
- islessequal (p, q): Den sjekker om p er mindre enn eller lik q eller ikke.
- isgreaterequal (p, q): Den sjekker om p er større enn eller lik q eller ikke.
- islessgeaker (p, q): Den sjekker om p er mindre eller større enn y eller ikke.
- isunordered (p, q): Den sjekker om p sammenlignet eller ikke.
C ++ kode for å implementere funksjonalitet ovenfor
#include
#include
using namespace std;
int main() (
// cout << less(22, 29) << "\n";
cout << isgreater(48, 47)<< "\n";
cout << islessequal(11, 5)<< "\n";
cout << isgreaterequal(19, 72)<< "\n";
cout << islessgreater(59, 84)<< "\n";
cout << isunordered(62, 84)<< "\n";
return 0;
)
Produksjon:

6. Bruke trigonometrisk funksjon
Funksjoner som er spesielt brukt i geometriske beregninger. Den rettvinklede trekanten gir en sammenheng mellom vinkel og forholdet mellom lengden på de to sidene.
- sin (y): Den vil beregne verdien av sin y.
- cos (y): Den vil beregne verdien til cosinus y.
- tan (y): Den vil beregne verdien av tangens y.
- asin (y): Den vil beregne verdien av invers sinus y.
- acos (y): Den vil beregne verdien av invers kosinus y.
- atan (y): Den vil beregne verdien av invers tangens y.
- atan2 (y, x): Den vil beregne verdien av den inverse tangenten til y- og x-koordinater.
C ++ kode for å implementere funksjonalitet ovenfor
#include
#include
using namespace std;
int main() (
cout << sin(0) << "\n";
cout << cos(0) << "\n";
cout << tan(1) << "\n";
cout << asin(1)<< "\n";
cout << acos(0)<< "\n";
cout << atan(1)<< "\n";
cout << atan2(0, 1)<< "\n";
return 0;
)
Produksjon:
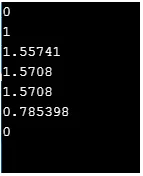
Her er noen mer interessante funksjoner som vil hjelpe til med å beregne verdier av hyperboliske trigonometriske funksjoner, og de kalles Hyperboliske funksjoner.
- sinh (x): Den vil beregne verdien av den hyperbolske sinusen til x.
- kosh (x): Den vil beregne verdien av den hyperbolske kosinus til x.
- tanh (x): Den vil beregne verdien av den hyperbolske tangenten til x.
- asinh (x): Den vil beregne verdien av den hyperbolske bue-sinusen til x.
- acosh (x): Den vil beregne verdien av den hyperbolske bue-kosinus av x.
- atanh (x): Den vil beregne verdien av den hyperbolske bue-sinusen til x.
C ++ kode for å implementere funksjonalitet ovenfor
#include
#include
using namespace std;
int main() (
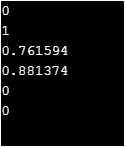
cout << sinh(0)<< "\n";
cout << cosh(0)<< "\n";
cout << tanh(1)<< "\n";
cout << asinh(1)<< "\n";
cout << acosh(1)<< "\n";
cout << atanh(0)<< "\n";
return 0;
)
Produksjon:
Konklusjon
Mattefunksjoner spiller en viktig rolle i å spare enorm tid og rom i minnet. Alle funksjonene er innebygde, ikke nødvendig å implementere direkte bruke noen matematikkfunksjon bare ved å legge til en overskriftsfil som vil gi muligheten til å bruke hele biblioteket i matematikklasse.
Anbefalte artikler
Dette er en guide til matematiske funksjoner i C ++. Her diskuterer vi at C ++ gir et stort antall forskjellige typer mattefunksjoner med eksempler. Du kan også gå gjennom andre foreslåtte artikler -
- Overstyring i C ++
- Overbelastning i C ++
- Firkantet rot i C ++
- Arrays i C ++
- Overbelastning i Java
- Square Root i PHP
- Topp 11 funksjoner og fordeler med C ++
- Guide to Square Root i JavaScript