Introduksjon til Heap Sort in C
Sortering er en teknikk som handler om bestilling av elementer basert på forskjellige egenskaper. (Egenskaper som å ordne data i stigende, synkende eller alfabetiske ordrer). Et hovedeksempel på sortering som vi kan tenke på her er bestilling av varer under online shopping. Vi kan forholde oss til priser, popularitet, siste og så videre. Så det er mange teknikker for denne plasseringen av elementer gjennom sortering. I dette emnet skal vi lære om Heap Sort i C.
Her skal vi lære en av de vanligste sorteringsteknikkene, Heap Sort, gjennom C-programmeringsspråk.
Logikken for Heap Sort
Hvordan kan vi faktisk utføre heap sortering? La oss sjekke ut nedenfor.
For det første er dyngen en av den trebaserte datastrukturen. Treet involvert her er alltid et komplett binærtre. Og det er to typer haug
- Min - Heap: Generelt arrangert i stigende rekkefølge, det vil si hvis overordnede elementet har en verdi som er mindre enn verdien av underordnede elementer.
- Max - Heap: Generelt arrangert i synkende rekkefølge, det vil si hvis overordnede elementelement har verdi mer enn for barnesnodeelementer.
Trinn for Heap Sort
- Når en usortert listedata er innhentet, organiseres elementer i massedatasstrukturen, enten basert på å lage en min-haug eller en maks-haug.
- Det første elementet fra listen over er lagt til i vårt utvalg
- Igjen danner hodet datatruktur teknikk som det samme som det første trinnet, og igjen blir enten det høyeste elementet eller det minste element plukket opp og lagt til i vårt utvalg.
- Gjentatte trinn hjelper oss med å få matrisen med den sorterte listen.
Program for Heap Sort in C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Først ber vi brukeren legge inn antall elementer som blir tatt for sortering, og deretter får brukeren oppgi forskjellige elementer som skal sorteres.
Trinn fulgt
- Det neste vi fokuserer på er å lage en heap-array, i dette tilfellet max-heap-array.
- Hovedbetingelsen for å få en maksimal heap-matrise er å sjekke at ingen foreldreknuteverdi er mindre enn dens barnesnudeverdi. Vi kommer til å bytte til vi oppnår den tilstanden.
- Den største fordelen med dette komplette binære treet er at de venstre og høyre barnesnutene til en overordnet node kan nås med verdiene 2 (i) + 1 og 2 * (i) + 2 verdier. Hvor jeg er overordnede noder.
- Så, på den måten her, plasserer vi rotnoden vår som inneholder maksimalverdien på høyre side av noden. Og deretter igjen etter samme prosedyre slik at neste maksimale antall nå blir rotnoden.
- Vi kommer til å følge den samme prosedyren til bare en node er igjen i haugarrayen.
- Og så arrangerer vi massegruppen vår for å danne et perfekt sortert utvalg i økende grad.
- Til slutt skriver vi ut den sorterte matrisen i utdataene.
Produksjon:
Utgangen er festet nedenfor.
La meg vise deg den billedlige representasjonen av hendelsene:
- De angitte dataene blir først representert i form av en endimensjonal matrise som følger.

- Den billedlige representasjonen av det binære treet som er dannet, er som følger:
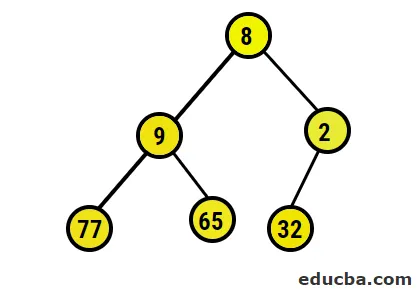
- Nå skal vi konvertere til maksimal haugen ved å sørge for at alle overordnede noder alltid er større enn underordnede noder. Som nevnt i utdataene under heap-sortert matrise, vil den billedlige representasjonen være:
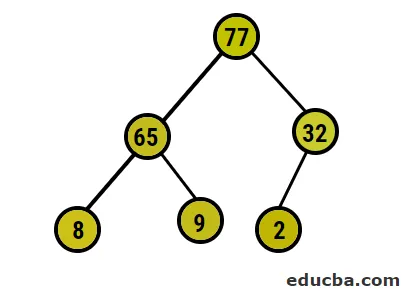
- Etter dette skal vi bytte rotnoden med den ekstreme bladnoden og deretter slette den fra treet. Bladknuten ville være roten nå og igjen samme prosess som ble fulgt for igjen å få det høyeste elementet i roten
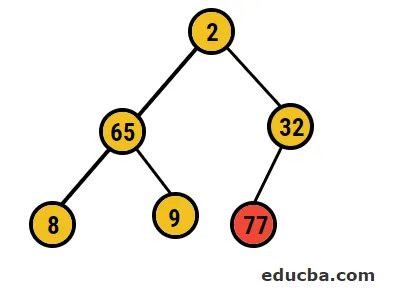
- Så i dette tilfellet blir 77 sifre slettet fra dette treet og plassert i vår sorterte gruppe, og prosessen gjentas.
Ovennevnte har vi sett det for å danne maksimal masse. Den samme prosessen blir også behandlet med dannelsen av min-hop-array. Som diskutert ovenfor, er den eneste forskjellen i forholdet mellom foreldre og barn nodeelementer.
Som en øvelse, kan du prøve å forme dyngen i fallende rekkefølge?
Konklusjon
Selv om det er mange sorteringsteknikker, regnes heap sortering som en av de bedre sorteringsteknikkene på grunn av tid og romkompleksitet. Tidskompleksiteten for alle beste, gjennomsnittlige og verste tilfeller er O (nlogn), der worst-case-kompleksiteten er bedre enn worst case-kompleksiteten til Quicksort og romkompleksiteten er O (1).
Anbefalte artikler
Dette er en guide til Heap Sort in C. Her diskuterer vi logikken og Steps for Heap Sort med eksempelskoden og utdata sammen med billedlige fremstillinger. Du kan også se på følgende artikler for å lære mer -
- Heap Sort In Java
- Valg Sorter i Java
- Palindrome in C-programmet
- Mønstre i C-programmering
- Heap Sort in C ++ (algoritme)
- Heap Sort in Python
- C Programmering av matrixmultiplikasjon