
Aritmetisk middelformel (innholdsfortegnelse)
- Formel
- eksempler
- Kalkulator
Hva er den aritmetiske middelformelen?
Begrepet "aritmetisk middelverdi" refererer i utgangspunktet til det matematiske gjennomsnittet av to eller flere tall. Metoden for å beregne det aritmetiske gjennomsnittet kan imidlertid variere basert på frekvensen til hver variabel i datasettet - enkelt gjennomsnitt (like vektet) eller vektet gjennomsnitt. Formelen for det aritmetiske gjennomsnittet for like vektede variabler kan avledes ved å oppsummere alle variablene i datasettet og deretter dele resultatet med antall variabler. Matematisk er det representert som,
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
eller
Arithmetic Mean =∑ x i / n
Hvor,
- x i = i variabelen
- n = Antall variabler i datasettet
Ved ulik vektede variabler kan formelen for det aritmetiske middelet avledes ved å oppsummere produktene til hver variabel og dens frekvens, og deretter blir resultatet delt på summen av frekvensene. Matematisk er det representert som,
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
eller
Arithmetic Mean = ∑ (f i * x i ) / f i
Hvor
- x i = i variabelen
- f i = Frekvens av den i variabelen
Eksempler på aritmetisk middelformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av aritmetisk middel på en bedre måte.
Du kan laste ned denne Arithmetic Mean Formula Excel Template her - Arithmetic Mean Formula Excel TemplateAritmetisk middelformel - eksempel # 1
La oss ta et eksempel på en batsman som scoret følgende løp i sine 10 siste omganger i løpet av det siste året: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Beregn batmanens gjennomsnitt i det siste 10 omganger.
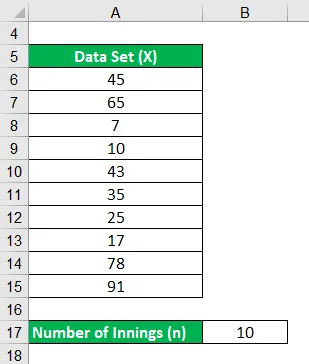
Løsning:
Aritmetisk middel beregnes ved å bruke formelen gitt nedenfor
Aritmetisk middel = ∑ x i / n
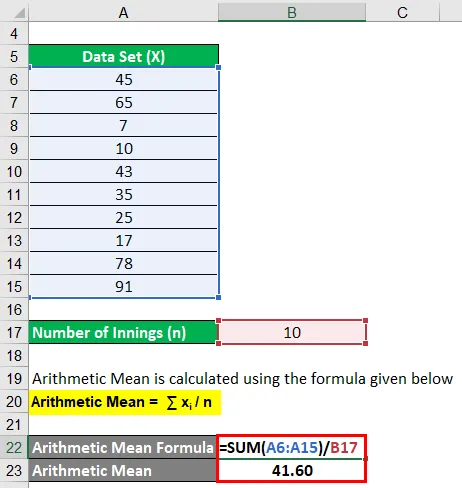
- Aritmetisk middel = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Aritmetisk gjennomsnitt = 41, 60
Derfor forble batmanens gjennomsnitt 41, 60 runder per omgang i de siste 10 omgangene.
Aritmetisk middelformel - eksempel # 2
La oss ta et eksempel på en klasse med 45 elever. Nylig ble det gjennomført en ukentlig test for naturfag der studentene ble evaluert på skalaen 1 til 10. Basert på følgende informasjon beregne gjennomsnittskarakterene i testen.
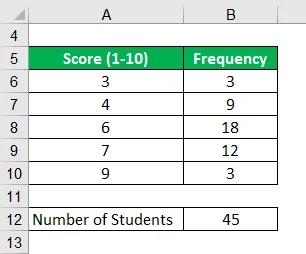
Løsning:
Aritmetisk middel beregnes ved å bruke formelen gitt nedenfor
Aritmetisk middel = ∑ (f i * x i ) / f i
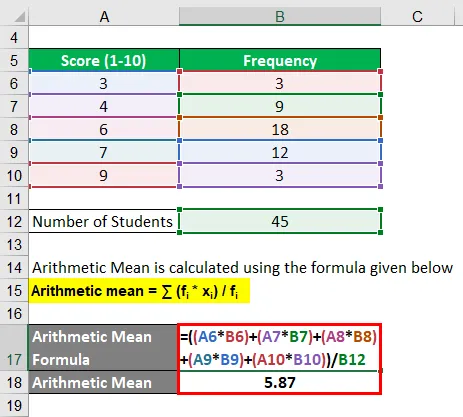
- Aritmetisk middel = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Aritmetisk gjennomsnitt = 264/45
- Aritmetisk middelverdi = 5, 87
Derfor var gjennomsnittlig poengsum for klassen i naturfagprøven 5, 87.
Aritmetisk middelformel - eksempel # 3
La oss ta et eksempel på to datasett med to forskjellige aritmetiske midler. Det første datasettet har 10 variabler med et gjennomsnitt på 45, mens det andre datasettet har 7 variabler og et gjennomsnitt på 42. Bestem det aritmetiske gjennomsnittet av de to datasettene kombinert.
Løsning:
Aritmetiske midler for det kombinerte datasettet beregnes ved å bruke formelen nedenfor
Aritmetisk middel = ((m 1 * n 1 ) + (m 2 * n 2 )) / (n 1 + n 2 )
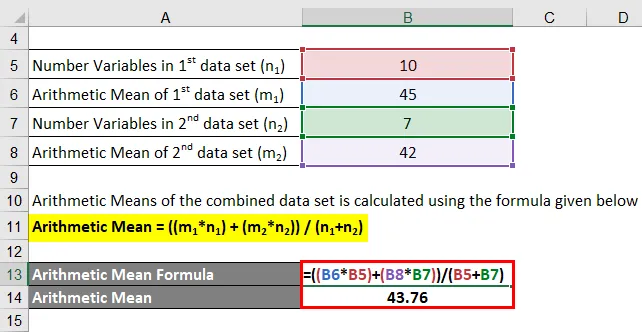
- Aritmetisk middel = (45 * 10 + 42 * 7) / (10 + 7)
- Aritmetisk gjennomsnitt = 43, 76
Derfor er det aritmetiske middelet til det kombinerte datasettet 43, 76.
Forklaring
Formelen for aritmetisk gjennomsnitt kan beregnes ved å bruke følgende trinn:
Trinn 1: Først skal du samle og sortere variablene som det aritmetiske middelet må beregnes for. Variablene er betegnet med x i .
Trinn 2: Finn deretter antall variabler i datasettet, og det betegnes med n i tilfelle like vektede variabler. Ellers må du finne ut frekvensen til hver variabel, og de er betegnet med f i, og antall variabler er summeringen av frekvensene.
Trinn 3: Endelig kan formelen for det aritmetiske gjennomsnittet for like vektede variabler avledes ved å legge til alle variablene, og deretter blir resultatet delt på antall variabler i datasettet som vist nedenfor.
Aritmetisk middel = ∑ x i / n
I tilfelle av vektet gjennomsnitt kan formelen for det aritmetiske gjennomsnitt imidlertid avledes ved å oppsummere produktene til hver variabel og dens frekvens, og deretter blir resultatet delt på summen av frekvensene som vist nedenfor.
Aritmetisk middel = ∑ f i * x i / f i
Relevans og bruk av aritmetiske middelformler
Begrepet aritmetisk middelverdi er veldig enkelt og elementært. Men det er fortsatt veldig viktig, siden det ofte blir brukt som en statistisk indikator for å vurdere det gjennomsnittlige utfallet i et datasett. Det tillater faktisk å evaluere hvilke av variablene som er bedre eller lavere enn gjennomsnittet av gruppen. Det brukes også som et mål for å representere gjennomsnittsverdien i hele dataserien. Videre brukes aritmetisk middel i tilfeller der geometriske middelverdier eller harmoniske midler er mindre nyttige, for eksempel gjennomsnittskarakter, vekt osv.
Aritmetisk gjennomsnittlig formelkalkulator
Du kan bruke følgende aritmetiske gjennomsnittskalkulator
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Aritmetisk gjennomsnitt | |
| Aritmetisk gjennomsnitt | = |
|
|
Anbefalte artikler
Dette er en guide til aritmetisk middelformel. Her diskuterer vi hvordan du beregner aritmetisk gjennomsnitt sammen med praktiske eksempler. Vi tilbyr også en aritmetisk middelkalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Hvordan beregne harmonisk middel?
- Guide to Population Mean Formula
- Beregning av gjennomsnitt ved bruk av formel
- Eksempler på netto salgsformel