
Introduksjon til binomial distribusjon i R
Denne artikkelen beskriver hvordan du bruker binomialfordelinger i R for de få operasjonene som er involvert med sannsynlighetsfordelinger. Forretningsanalyse bruker binomial sannsynlighet for et komplekst problem. R har mange innebygde funksjoner for beregning av binomialfordelinger brukt i statistisk interferens. Binomialfordelingen også kjent som Bernoulli-forsøk tar to typer suksess p og fiasko S. Hovedmålet med binomialfordelingsmodellen er at de beregner mulige sannsynlighetsutfall ved å overvåke et spesifikt antall positive muligheter ved å gjenta prosessen et bestemt antall ganger . De skal ha to mulige resultater (suksess / fiasko), derfor er utfallet dikotomt. Den forhåndsdefinerte matematiske notasjonen er p = suksess, q = 1-p.
Det er fire funksjoner assosiert med Binomial-distribusjoner. De er dbinom, pbinom, qbinom, rbinom. Den formaterte syntaks er gitt nedenfor:
syntax
- dbinom (x, størrelse, prob)
- pbinom (x, størrelse, prob)
- qbinom (x, størrelse, prob) eller qbinom (x, størrelse, prob, lavere_hale, log_p)
- rbinom (x, størrelse, prob)
Funksjonen har tre argumenter: verdien x er en vektor av kvantiler (fra 0 til n), størrelse er antall sporforsøk, prob angir sannsynlighet for hvert forsøk. La oss se en etter en med et eksempel.
1) dbinom ()
Det er en tetthets- eller distribusjonsfunksjon. Vektorverdiene må være et helt tall skal ikke være et negativt tall. Denne funksjonen prøver å finne et antall suksesser i et nei. av forsøk som er faste.
En binomialfordeling tar størrelse og x verdier. for eksempel størrelse = 6, de mulige x-verdiene er 0, 1, 2, 3, 4, 5, 6 som innebærer P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Produksjon:
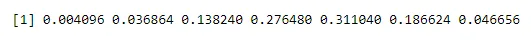
Gjør sannsynlighet for en
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Produksjon:
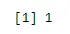
Eksempel 1 - Sykehusdatabasen viser at pasientene som lider av kreft, 65% dør av den. Hva er sannsynligheten for at 5 tilfeldig valgte pasienter hvorav 3 vil komme seg?
Her bruker vi dbinom-funksjonen. Sannsynligheten for at 3 vil komme seg ved bruk av tetthetsfordeling på alle punkter.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Produksjon:

For x verdi 0 til 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Produksjon:
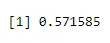
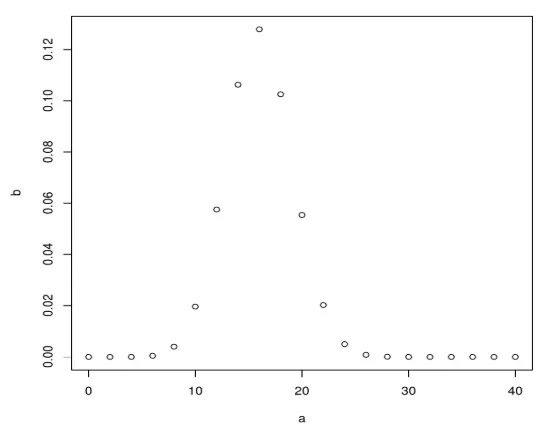
Deretter lager du en prøve på 40 papirer og øker med 2 og oppretter også binomial ved hjelp av dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Den produserer følgende utdata etter utførelse av koden ovenfor. Binomialfordelingen plottes med plot () -funksjonen.
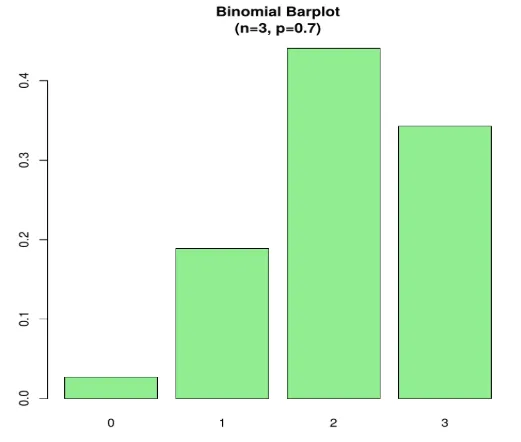
Eksempel 2 - Tenk på et scenario, la oss anta en sannsynlighet for at en student låner ut en bok fra et bibliotek er 0, 7. Det er 6 studenter på biblioteket. Hva er sannsynligheten for at 3 av dem låner ut en bok?
her P (X = 3)
Kode:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Under Plot viser når p> 0.5, er binomialfordeling derfor skjeve som vist.
Produksjon:
2) Pbinom ()
beregner kumulative sannsynligheter for binomial eller CDF (P (X <= x)).
Eksempel 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Produksjon:

Eksempel 2: Dravid scorer en wicket på 20% av forsøkene sine når han boller. Hvis han boller 5 ganger, hva er sannsynligheten for at han scorer 4 eller mindre wicket?
Sannsynligheten for suksess er 0, 2 her og i løpet av 5 forsøk vi får
pbinom(4, size=5, prob=.2)
Produksjon:
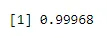
Eksempel 3: 4% av amerikanerne er svarte. Finn sannsynligheten for 2 svarte elever når du tilfeldig velger 6 elever fra en klasse på 100 uten erstatning.
Når R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Produksjon:-
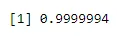
3) qbinom ()
Det er en kvantifunksjon og gjør det inverse av den kumulative sannsynlighetsfunksjonen. Den kumulative verdien samsvarer med en sannsynlighetsverdi.
Eksempel: Hvor mange haler vil ha en sannsynlighet på 0, 2 når en mynt kastes 61 ganger.
a <- qbinom(0.2, 61, 1/2)
print(a)
Produksjon:-
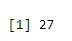
4) rbinom ()
Det genererer tilfeldige tall. Ulike utfall gir forskjellige tilfeldige resultater som brukes i simuleringsprosessen.
Eksempel:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Produksjon:-

Hver gang vi utfører gir det tilfeldige resultater.
rbinom(200, 4, 0.4)
Produksjon:-

Her gjør vi dette ved å anta utfallet av 30 myntflipper i et enkelt forsøk.
rbinom(30, 1, 0.5)
Produksjon:-
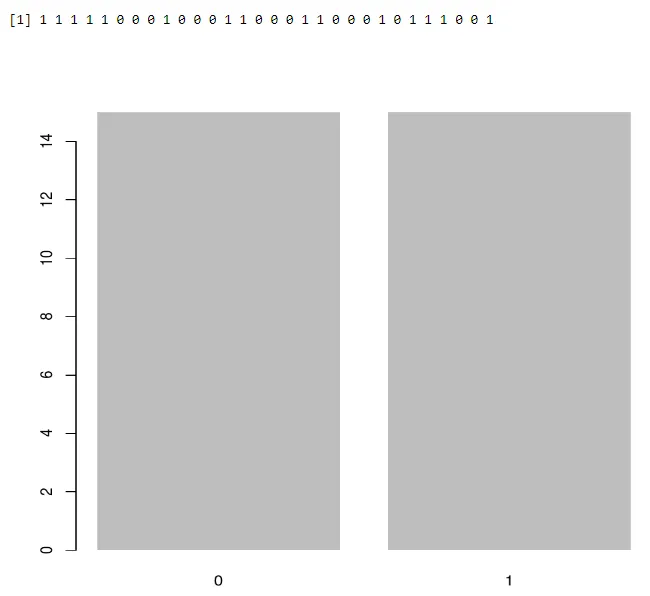
Bruker barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Produksjon:-
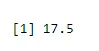
For å finne middelverdien for suksess
output <-rbinom(10, size=60, 0.3)
mean(output)
Produksjon:-
Konklusjon - Binomial distribusjon i R
I dette dokumentet har vi derfor diskutert binomial distribusjon i R. Vi har simulert ved hjelp av forskjellige eksempler i R studio og R-utdrag og også beskrevet de innebygde funksjonene som hjelper til med å generere binomiale beregninger. Binomial fordelingsberegning i R bruker statistiske beregninger. Derfor hjelper en binomialfordeling med å finne sannsynlighet og tilfeldig søk ved å bruke en binomvariabel.
Anbefalte artikler
Dette er en guide til Binomial distribusjon i R. Her har vi diskutert en introduksjon og dens funksjoner assosiert med Binomial distribusjon sammen med syntaks og passende eksempler. Du kan også gå gjennom andre foreslåtte artikler for å lære mer -
- Binomial distribusjonsformel
- Økonomi vs virksomhet
- Business Analytics-teknikker
- Linux-distribusjoner