Hypergeometrisk distribusjonsformel (innholdsfortegnelse)
- Formel
- eksempler
Hva er formler for hypergeometrisk distribusjon?
Den hypergeometriske fordelingen er i utgangspunktet en diskret sannsynlighetsfordeling i statistikk. Det ligner veldig på binomial distribusjon, og vi kan si at med tillit til at binomial distribusjon er en stor tilnærming for hypergeometrisk distribusjon bare hvis 5% eller mindre av befolkningen blir tatt ut. Hvis vi har tilfeldige tegninger, er hypergeometrisk distribusjon en sannsynlighet for suksesser uten å erstatte varen når den er tegnet. Men i en binomial fordeling beregnes sannsynligheten med erstatning. For eksempel har du en kurv som har N-baller hvorfra "n" er svarte, og du tegner "m" -kuler uten å bytte ut noen av ballene. Så hypergeometrisk fordeling er sannsynlighetsfordelingen for antall svarte kuler trukket fra kurven.
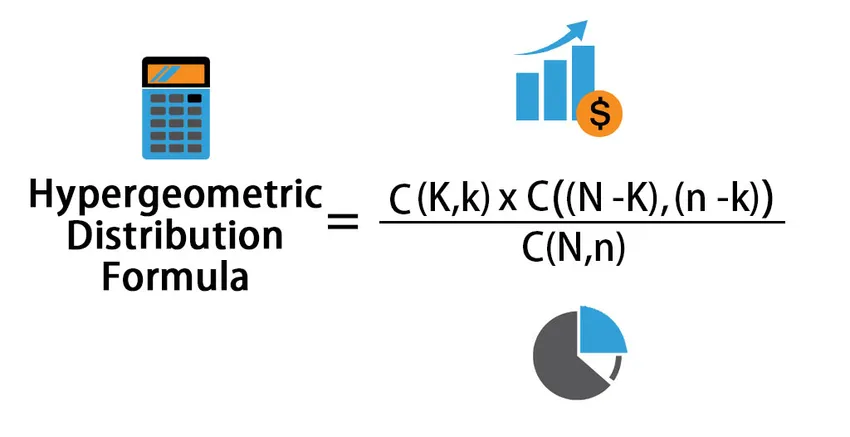
Formel for hypergeometrisk distribusjon:
Probability of Hypergeometric Distribution = C(K, k) * C((N – K), (n – k)) / C(N, n)
Hvor,
- K - Antall “suksesser” i befolkningen
- k - Antall "suksesser" i utvalget
- N - Befolkningsstørrelse
- n - Prøvestørrelse
For å forstå formelen for hypergeometrisk distribusjon, bør man være godt klar over binomialfordelingen og også kombinasjonsformelen.
Kombinasjonsformel:
C (n, r) = n! / (r! * (nr)!)
- n! - n factorial = n * (n-1) * (n-2) ……… .. * 1
- r! - r factorial = r * (r-1) * (r-2) ……… .. * 1
- (nr)! - (nr) factorial = (nr) * (nr-1) * (nr-2) ……… .. * 1
Eksempler på Hypergeometrisk distribusjonsformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av den hypergeometriske distribusjonen på en bedre måte.
Du kan laste ned denne Hypergeometric Distribution Formula Excel Template her - Hypergeometric Distribution Formula Excel TemplateHypergeometrisk distribusjonsformel - eksempel # 1
La oss si at du har et kortstykke fargede kort som har 30 kort hvorav 12 er svarte og 18 er gule. Du har trukket 5 kort tilfeldig uten å erstatte noen av kortene. Nå vil du finne sannsynligheten for at det trekkes nøyaktig tre gule kort.
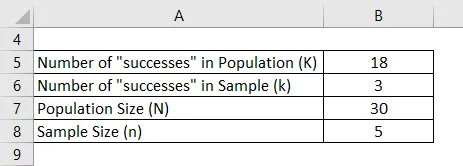
Løsning:
Hypergeometrisk distribusjon beregnes ved å bruke formelen nedenfor
Sannsynlighet for hypergeometrisk distribusjon = C (K, k) * C ((N - K), (n - k)) / C (N, n)
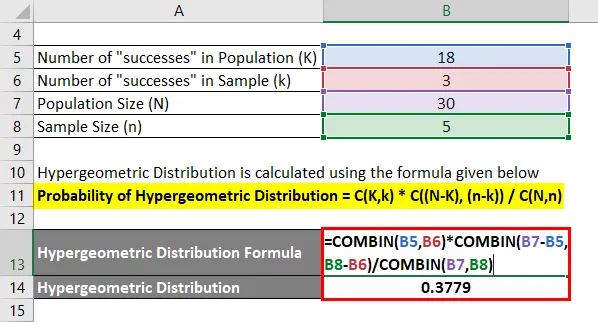
- Sannsynlighet for å få nøyaktig 3 gule kort = C (18, 3) * C ((30-18), (5-3)) / C (30, 5)
- Sannsynlighet for å få nøyaktig 3 gule kort = C (18, 3) * C (12, 2) / C (30, 5)
- Sannsynlighet for å få nøyaktig 3 gule kort = (18! / (3! * 15!)) * (12! / (2! * 10!)) / (30! / (5! * 25!))
- Sannsynligheten for å få nøyaktig 3 gule kort = 0.3779
Hypergeometrisk distribusjonsformel - eksempel # 2
La oss si at du bor i en veldig liten by som har 75 kvinner og 95 hanner. Nå var det avstemning som fant sted i byen din, og alle stemte. Et utvalg på 20 velgere ble valgt tilfeldig. Du vil beregne hva som er sannsynligheten for at nøyaktig 12 av disse velgerne var mannlige velgere.
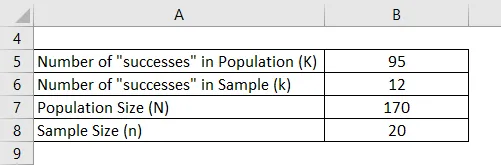
Løsning:
Hypergeometrisk distribusjon beregnes ved å bruke formelen nedenfor
Sannsynlighet for hypergeometrisk distribusjon = C (K, k) * C ((N - K), (n - k)) / C (N, n)
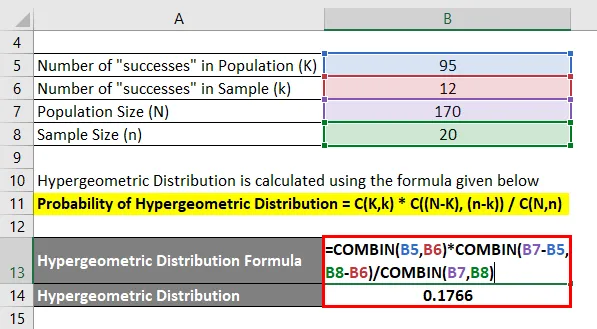
- Sannsynlighet for å få 12 mannlige velgere = C (95, 12) * C ((170-95), (20-12)) / C (170, 20)
- Sannsynlighet for å få 12 mannlige velgere = C (95, 12) * C (75, 8) / C (170, 20)
- Sannsynlighet for å få 12 mannlige velgere = (95! / (12! * 83!)) * (75! / (8! * 63!)) / (170! / (20! * 150!))
- Sannsynlighet for å få 12 mannlige velgere = 0.1766
Forklaring
Som diskutert ovenfor, er hypergeometrisk distribusjon en sannsynlighetsfordeling som er veldig lik en binomial fordeling med forskjellen at det ikke er noen erstatning tillatt i den hypergeometriske fordelingen. For å utføre denne typen eksperiment eller distribusjon er det flere kriterier som må oppfylles.
- Det første og det fremste kravet er at data som samles inn skal ha diskret karakter.
- Hver plukking eller tegning bør ikke erstattes av en annen, fordi når en tilfeldig variabel tegnes uten erstatning, er den ikke uavhengig og har forhold til hva som er tegnet tidligere.
- Det må være to sett med forskjellige grupper, og du vil vite sannsynligheten for et spesifikt antall medlemmer i en gruppe. I stemmereksemplet har vi for eksempel menn og kvinner. I poseeksempel har vi en gul og svart gruppe.
Sammen med disse forutsetningene spiller kunnskap om kombinasjon også en viktig rolle i å utføre hypergeometrisk distribusjon. Så det er viktig at man skal kjenne til begrepene om kombinasjon før man går videre til hypergeometrisk distribusjon.
Relevans og bruk av formler for hypergeometrisk distribusjon
Hypergeometrisk distribusjon har mange bruksområder i statistikk og i praktisk liv. Den vanligste bruken av den hypergeometriske fordelingen, som vi har sett ovenfor i eksemplene, er å beregne sannsynligheten for prøver når de trekkes fra et sett uten erstatning. I det virkelige livet er det beste eksemplet lotteriet. Så i et lotteri, når tallet først er ute, kan det ikke gå tilbake og kan erstattes, så hypergeometrisk distribusjon er perfekt for denne typen situasjoner.
Anbefalte artikler
Dette er en guide til Hypergeometrisk distribusjonsformel. Her diskuterer vi Hvordan beregne hypergeometrisk distribusjon sammen med praktiske eksempler. Vi tilbyr også en nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Guide to Standard Normal Distribution Formula
- Kalkulator for formel for hypotesetesting
- Formel for returperiode
- Variansanalyseformel med Excel-mal