
Forskjell mellom Z-score vs T-score
Z-poengsum er en konvertering av rå data til en standard score, når konverteringen er basert på populasjonsmidlet og populasjonsstandardavviket. Når et komplett datasett er tilgjengelig hos oss, kan vi beregne Z-poengsummen. Z-poengsum er subtraksjon av populasjonsgjennomsnittet fra rå poengsum og deler deretter resultatet med populasjonsstandardavvik. T-poengsum er en konvertering av rådata til standard-poengsum når konverteringen er basert på eksempelmidlet og standardstandardavviket. Når populasjonsdatasettet ikke er tilgjengelig, må vi plukke opp noen eksempeldata for å beregne eksempelmidlet og populasjonsstandardavviket.
Z-poengsum
Under en normal fordeling, hvor full data er tilgjengelig, er det en avstand fra gjennomsnittet. Formelen er som gitt nedenfor,
Z= (x-μ)/σ
Hvor,
X = individuelle rådata
μ = Befolkningsgjennomsnitt
σ = Befolkningsstandardavvik
T score
T-poengsum er subtraksjon av individuelt standardavvik fra individuelt gjennomsnitt og del deretter resultatet med prøvestandardavvik hele resultat multiplisert med prøvestørrelse. Formelen er som gitt nedenfor,
t = ((- μ)/s)*
= Eksempel middel
μ = Befolkningsgjennomsnitt
s = Eksempel Standardavvik
n = prøve størrelse
La oss ta et eksempel for å forstå det samme på en bedre måte:
I en artikkel er 3 underavdelinger der- I, II og III. La antall studenter som svarte jeg være riktig, 25%, dvs. 75% klarer ikke å svare riktig. Tilsvarende, la 10% og 20% av antallet personer som hadde svart seksjon II og III riktig, 90% og 80% har imidlertid funnet seksjon II og III skjønt. Vi antar at evnen målt av disse tre elementene er den samme og at den normalt distribueres,
Poengsummen for hver elev i en klasse brukes til å beregne gjennomsnittet av karakterer som er lik 50 og et standardavvik på 10. Vi kan beregne Z-poengsum med poengsummen 50 som (50-50) / 10 = 0
Vi kan tolke at studentens poengsum er 0 avstand (i enheter av standardavvik) fra gjennomsnittet, slik at studenten har scoret gjennomsnitt.
Hvis poengsummen er 60, er Z-poengsummen (60-50) / 10 = 1
Vi kan tolke at studenten har scoret over gjennomsnittet - en avstand på 1 standardavvik over gjennomsnittet.
Sammenligning av topp til hodet mellom Z-score og T-score (Infographics)
Nedenfor er topp 9-forskjellen mellom Z-score og T-poengsum 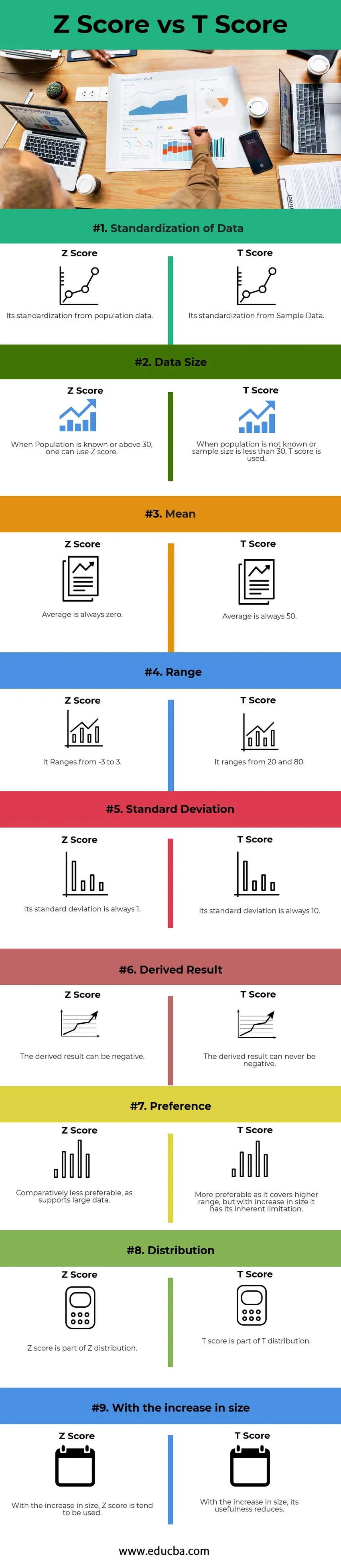
Viktige forskjeller mellom Z-score og T-poengsum
La oss diskutere noen av de viktigste forskjellene mellom Z-score og T-poengsum
- Z-score er standardiseringen fra populasjonsrådata eller mer enn 30 eksempeldata til standard score, mens T-score er standardisering fra eksempeldata på mindre enn 30 data til standard score
- Z-poengsum varierer fra -3 til 3, mens T-poengsum varierer fra 20 til 80.
- Når datastørrelsen øker, har distribusjon en tendens til å være Z-distribusjon. Begge Z-score vs T-poengsfordeling er en del av en normalfordeling, men basert på størrelsen skiller de seg fra hverandre
- Rent praktisk blir Z-score i stor utstrekning brukt i aksjemarkedsdata og for å sjekke sjansene for at et selskap går i konkurs, mens t-poengsum blir mye brukt for å sjekke benmineraltetthet og brudd på risikovurderinger
Z-score vs T-score Sammenligningstabell
La oss se på topp 9-sammenligning mellom Z-score og T-poengsum
| Sr. Nei. | Sammenligningspunkter | Z Score | T score |
| 1 | Standardisering av data | Det er standardisering fra populasjonsdata | Det er standardisering fra eksempeldata |
| 2 | Datastørrelse | Når befolkningen er kjent eller over 30, kan man bruke Z-poengsum | Når populasjonen ikke er kjent eller prøvestørrelsen er mindre enn 30, brukes T-poengsum. |
| 3 | Mener | Et gjennomsnitt er alltid null. | Et gjennomsnitt er alltid 50. |
| 4 | Område | Det varierer fra -3 til 3. | Det spenner fra 20 og 80. |
| 5 | Standardavvik | Standardavviket er alltid 1 | Standardavviket er alltid 10 |
| 6 | Avledet resultat | Det avledede resultatet kan være negativt | Det avledede resultatet kan aldri være negativt |
| 7 | Preference | Forholdsvis mindre å foretrekke, som støtter store data | Mer foretrukket ettersom det dekker et høyere område, men med en økning i størrelse har det sin iboende begrensning |
| 8 | Fordeling | Z-score er en del av Z-distribusjonen | T-score er en del av T-distribusjonen |
| 9 | Med økningen i størrelse | Med økningen i størrelse, pleier Z-poengsum å bli brukt | Med økningen i størrelse reduserer nytten. |
Konklusjon
Begge Z-score vs T-score er en del av hypotesetesting under normalfordeling. Hvis du har et sett med målescore på forskjellige målinger ved å bruke Z-poengsummer, kan du fortelle hvordan score er plassert i fordelingen. Så kan du sammenligne dem. Standardisering av score er en mye brukt prosedyre innen forskning og planlegging, da de hjelper i sammenligning av forskjellige testresultater. Standardisering av score før du kombinerer dem hjelper en forsker med å få bedre og sammenlignbare resultater.
Anbefalte artikler
Dette har vært en guide til den største forskjellen mellom Z-score og T-poengsum. Her diskuterer vi også Z-poengsummen vs T-score viktige forskjeller med infografikk og sammenligningstabell. Du kan også se på følgende artikler for å lære mer-
- Finans vs økonomi - Topp forskjell
- Underskudd kontra gjeld - hvilken som er bedre
- Eiendomskjøp kontra aksjekjøp
- Pengemarked vs kapitalmarked
- Oversikt over Altman Z Score