RATE Formel i Excel

Excel RATE-formel (innholdsfortegnelse)

RATE Formel i Excel
Hvordan bruker jeg RATE-formel i Excel?

Denne RATE-formelen gir renten for en periode per annuitet. RATE-funksjonen beregner gjentatte ganger for å finne frekvensen for den perioden. RATE-funksjonen kan brukes til å finne en rente for en periode, og kan deretter multipliseres for å finne den årlige renten. Så denne formelen kan brukes til å utlede renten. Formelen for denne funksjonen er som følger.

= RATE (nper, pmt, pv, (fv), (type), (guess))

Nedenfor er forklaringen på de gitte argumentene:

nper - Antall betalingsperioder for en livrente. (Påkrevd)
pmt - Betaling som skal utføres for hver periode, dette vil bli løst. (Påkrevd)
pv - Nåverdi, totalt beløp som en serie av fremtidig betaling er verdt nå. (Påkrevd)
fv - Future Value, Målbeløp å ha etter den påfølgende avbetalingen, hvis vi ekskluderer fv kan vi ta 0 i stedet. (Valgfri)
type - Dette undersøker hvordan funksjonen vil vurdere forfallsdato for betaling, så vi må sette dette i binær 0 eller 1, 0 betyr at betaling som skal betales ved periodens slutt. (Valgfri)
gjetning - Dette argumentet brukes til å gjette renten. Den vil gi hastighetsfunksjonen en start før du når 20 iterasjoner. Det er to muligheter for dette argumentet når det utelukkes antar at vårt gjetning er 10%, ellers vil den prøve andre verdier for input (valgfritt).

Hvordan bruker jeg RATE-formel i Excel?

Vi vil nå lære hvordan du skriver RATE-formel for å få oppslagverdien. La oss forstå denne formelen med noen eksempler.

Du kan laste ned denne RATE Formula Excel Template her - RATE Formula Excel Template

Eksempel 1

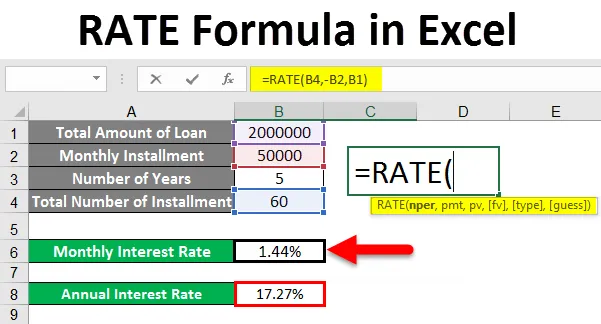
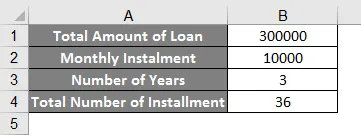
For dette eksempelet, antar du at du vil kjøpe en bil, og prisen på den bilen er 3, 00 000, 00 INR. Og du

gikk til en bankmann og ba om et billån, du ble sagt at du må betale INR 10.000, 00 pr

måned i 3 år (36 måneder)

Her er dette situasjonen hvor vi kan bruke RATE-funksjonen vår til å finne rentesatsen for den gitte

betingelse.

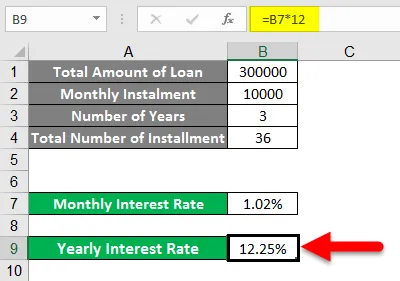
Nå i henhold til bildet nedenfor kan du se at vi har nevnt detaljene vi har, Nå i utgangspunktet

finner vi rentesatsen per måned og deretter i et år ved å multiplisere den med 12.

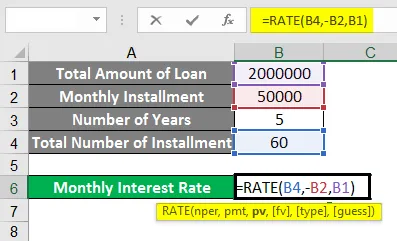
Nå kan du se fra bildet under kan du se at vi har brukt formelen for RATE er som

følger:

= RATE (B5, -B3, B2)

Her er argumentene:

nper = B5 (Totalt antall avdrag)

pmt = -B3 (betaling for hvert avdrag)

pv = B2 (lånebeløp)

Her kan du legge merke til at pmt (B3) er tatt negativt fordi beregningen er fra låntakers

perspektiv, så dette er det månedlige avbetalingsbeløpet som er kontantstrømmen for den enkelte

(Låntaker) må betale hver måned. Så låntakeren mister dette beløpet hver måned, det er det

årsaken til at det er negativt.

Hvis vi nå beregner dette lånet fra bankens perspektiv, ettersom banken månedlig gir lånet til låntageren, vil (B2) lånebeløpet være negativt, fordi banken på hver avdrag må betale det mindre til låntaker månedlig, så i henhold til perspektivet må vi endre det negative tegnet i formelen.
Nå kan du se at ved å bruke denne funksjonen har vi funnet renten hvis renten er månedlig (I vårt tilfelle er den 1, 02%).

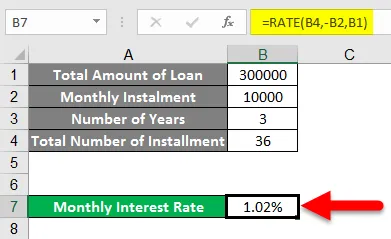
Og ved å multiplisere den med 12 kan vi ha renten årlig (i vårt tilfelle er den 12, 25%).

Eksempel 2

I likhet med eksemplet ovenfor for praksis vil vi se et annet eksempel der vi må finne renten. I henhold til bildet nedenfor er dataene vi har for å finne renten.

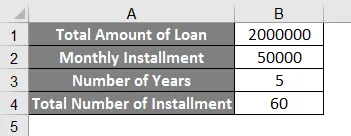
Her har vi 20 laks å betale med 50 tusen per måned i 5 år (60 avdrag).
Så argumentene er som følger:

nper = 20 lakker

pmt = 50.000

pv = 60 avdrag (5 år)

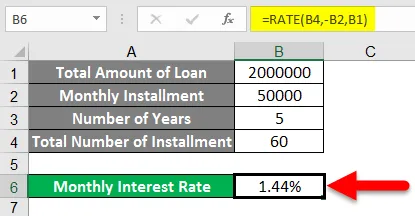
I henhold til bildet over kan vi se at RATE-funksjonen er brukt og funnet at den månedlige rentesatsen er 1, 44%
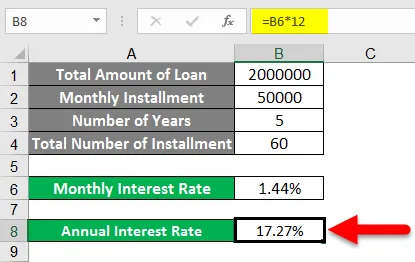
Nå ved å multiplisere den med 12 vil vi få den årlige renten som er 27% for det gitte eksempelet.

Eksempel 3

For dette eksempelet, antar vi at vi kjenner renten og avdragsnumrene, men vi vil finne ut hvor stor en månedlig avbetaling er.
Her for dette eksempelet har vi tatt følgende data i henhold til bildet nedenfor:

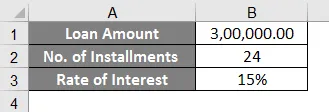
Vi har tatt et lån på 3 laks til 15% av renten (årlig), her vet vi renten, men vi trenger å finne pmt: beløp som skal betales for hvert avdrag.
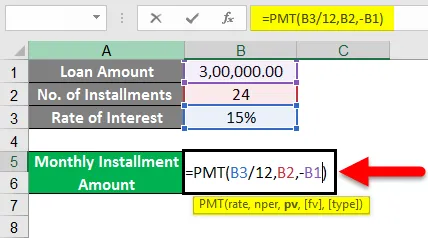
Som vi kan se fra bildet under, er formelen for pmt som følger:

= pmt (B4 / 12, B3, -B2)

Vi kan merke noe her at vi har tatt B4 / 12, dette fordi renten som er gitt til oss er per år (årlig), så ved å dele den med 12 lager vi den månedlig.

Så som vi kan se bildet under, vil det månedlige avbetalingsbeløpet være $ 14, 545.99 for å være nøyaktig.

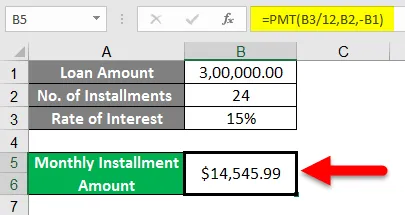
I henhold til eksemplet ovenfor har vi funnet et av argumentene våre for RATE-funksjon.

Ting å huske på RATE Formula

#NUM! Feil :

Denne feilen kan oppstå når resultatet av frekvensen ikke konvergerer innen 0.0000001 for 20 iterasjoner. Det kan skje når vi ikke nevner kontantstrømskonveksjon ved å tilordne det negative tegnet til det aktuelle argumentet i formelen, i henhold til eksemplet ovenfor har vi sett at når vi beregner satsen for låntakersiden, får det månedlige avdragsbeløpet et negativt tegn på grunn av månedlig kontantstrøm for låntakeren. Så hvis vi ikke bruker det negative tegnet på den månedlige kontantstrømmen, vil vi støte på denne feilen.

Så her kan vi sette gjetningsargument for å fungere, fordi det vil tillate oss å starte ettersom det må konvergere innen 20 iterasjoner og gi oss det nærmere eller til og med riktige svaret.
Alle argumenter skal være numeriske, ellers vil den støte på #value-feilen.
Med RATE-funksjonen når du beregner renten for de gitte dataene, finner vi rentene per måned. Så for å konvertere det i årlig rente, må vi multiplisere det med 12.

Anbefalte artikler

Dette har vært en guide til RATE Formula i Excel. Her diskuterte vi hvordan du bruker RATE Formula i Excel sammen med praktiske eksempler og nedlastbar Excel-mal. Du kan også gå gjennom andre foreslåtte artikler -

Hvordan bruke Square Root-funksjon i Excel?
QUOTIENT-funksjon i Excel
Hvordan dele tall ved å bruke formel i Excel?
Pakk inn tekstfunksjon i Excel

RATE Formel i Excel - Hvordan bruke RATE-formler i Excel?

Innholdsfortegnelse: