
Introduksjon til funksjoner i R
Funksjonen er definert som et sett med uttalelser, for å utføre og utføre enhver spesifikk logisk oppgave. Funksjon tar noen inndataparametere som er kjent som argumenter for å utføre oppgaven. Funksjoner hjelper til med å bryte koden, til enklere biter ved å orkestreere den logisk, noe som er lettere å lese og forstå. I dette emnet skal vi lære om funksjoner i R.
Hvordan skrive funksjoner i R?
For å skrive funksjonen i R, her er syntaks:
Fun_name <- function (argument) (
Function body
)
Her kan man se “funksjons” spesifikt reservert ord brukes i R, for å definere hvilken som helst funksjon. Funksjonen tar innspill som er i form av argumenter. Funksjonsorganet er et sett med logiske utsagn som utføres over argumenter, og deretter returnerer det resultatet. “Fun_name” er navnet som er gitt til funksjonen, gjennom hvilken den kan kalles hvor som helst i R-programmet.
La oss se et eksempel, som vil være mer klar når det gjelder forståelse av funksjonsbegrepet i R.
R-kode
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
produksjon:
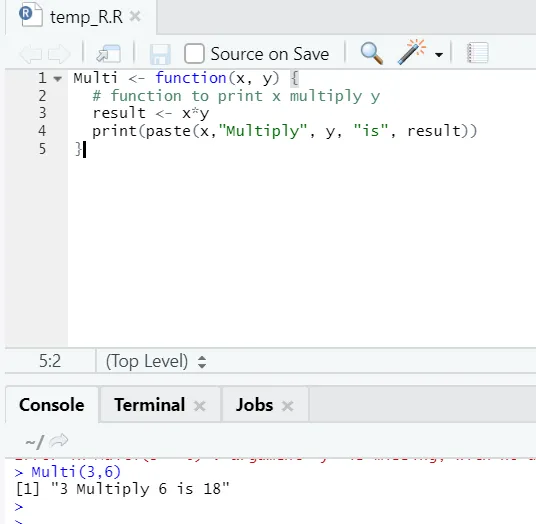
Her opprettet vi funksjonsnavnet “Multi”, som tar to argumenter som innganger og gir den multipliserte utgangen. Det første argumentet er x og det andre argumentet er y. Som du ser, har vi kalt funksjonen under navnet “Multi”. Her hvis noen vil, kan argumenter også settes til standardverdien.
Ulike typer funksjoner i R
Ulike R-funksjoner med syntaks og eksempler (innebygd, matematikk, statistisk osv.)
1) Innebygd funksjon -
Dette er funksjonene som følger med R for å adressere en spesifikk oppgave ved å ta et argument som input og gi en output basert på den gitte inputen. La oss diskutere noen viktige generelle funksjoner ved R her:
a) Sortering: Data kan være av typen til stigende eller synkende rekkefølge. Data kan være om en vektor av fortsettelsesvariabel eller faktorvariabel er.
syntaks:

Her er forklaringen på parametrene:
- x: Dette er en vektor for den kontinuerlige variabelen eller faktorvariabelen
- synkende: Dette kan settes enten sant / usant til å kontrollere rekkefølge ved å stige opp eller ned. Som standard er det FALSE`.
- sist: Hvis vektoren har NA-verdier, skal den settes sist eller ikke
R-kode og utgang:
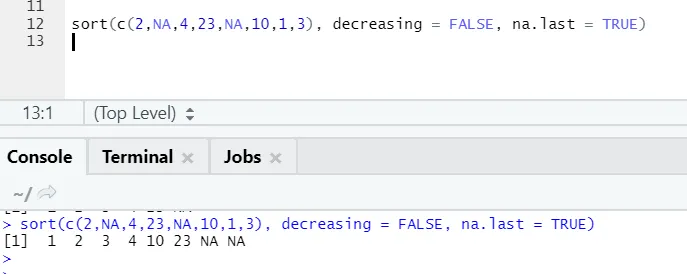
Her kan man legge merke til hvordan “NA” -verdier blir justert på slutten. Som vår parameter na.last = True var sant.
b) Sekvens: Det genererer en sekvens av tallet mellom to spesifiserte tall.
syntax
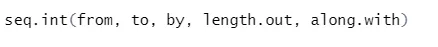
Her er forklaringen på parametrene:
- fra, til start og slutt verdi av sekvensen.
- av: Økning / gap mellom to påfølgende tall i rekkefølge
- length.out: den nødvendige lengden på sekvensen.
- Along.with: Henviser til lengden fra lengden på dette argumentet
R-kode og utgang:
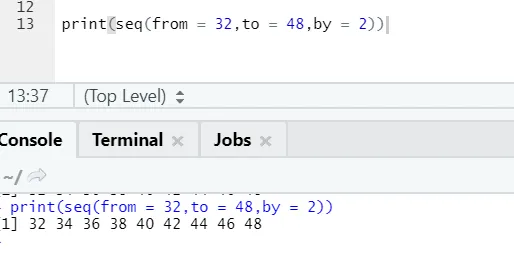
Her kan man legge merke til at sekvensen som genereres har inkrementering av 2 fordi by er definert som 2.
c) Toupper, tolower: De to funksjonene: toupper og tolower er funksjoner som brukes på strengen for å endre sakene til bokstavene i setninger.
R-kode og utgang:
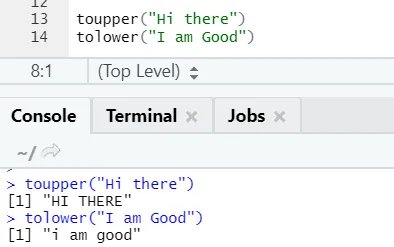
Man kan legge merke til hvordan sakene med brev blir endret når de brukes på funksjonen.
d) Rnorm: Dette er en innebygd funksjon som genererer tilfeldige tall.
R-kode og utgang:
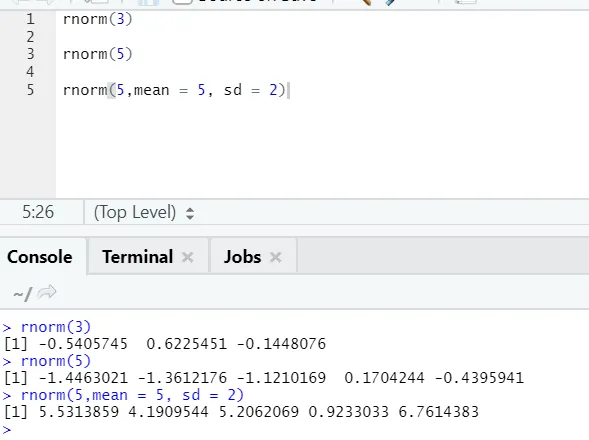
Funksjonen rnorm tar det første argumentet som sier hvor mange tall som må genereres.
e) Rep: Denne funksjonen gjenskaper verdien så mange ganger som spesifisert.
R syntaks: rnorm (x, n)
Her representerer x verdi som skal replikeres, og n representerer antall ganger den må replikeres.
R-kode og utgang:
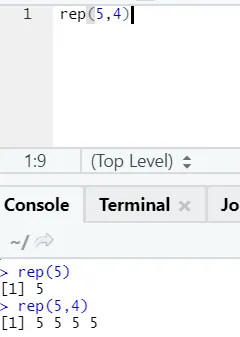
f) Lim inn: Denne funksjonen er å koble sammen strenger med en bestemt karakter i mellom.
syntaks
paste(x, sep = “”, collapse = NULL)
R-kode
paste("fish", "water", sep=" - ")
R-utgang:
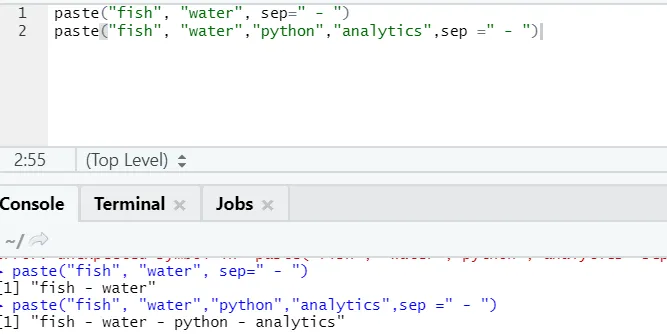
Som du kan se, kan vi lime inn mer enn to strenger også. Sep er den spesifikke karakteren som vi la til mellom strengene. Som standard er september plass.
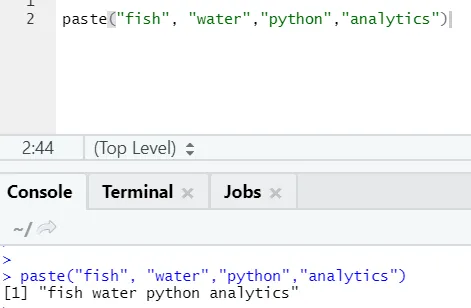
En annen lignende funksjon eksisterer som denne, som alle bør være klar over er paste0.
Funksjonspasta0 (x, y, kollaps) fungerer som lime (x, y, sep = “”, kollaps)
Se eksemplet nedenfor:
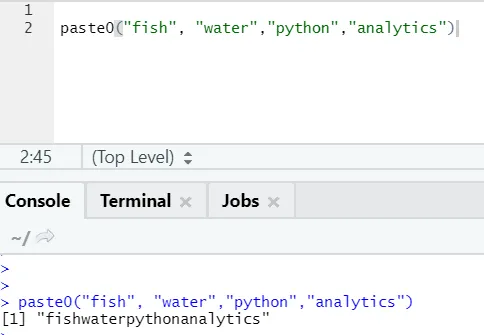
Med enkle ord for å oppsummere lime og lime0:
Lim 0 er raskere enn lim når det kommer til sammenføyning av strenger uten noen separator. Ettersom lim alltid ser etter “sep” og som som standard er plass i den.
g) Strsplit: Denne funksjonen er å dele strengen. La oss se de enkle tilfellene:
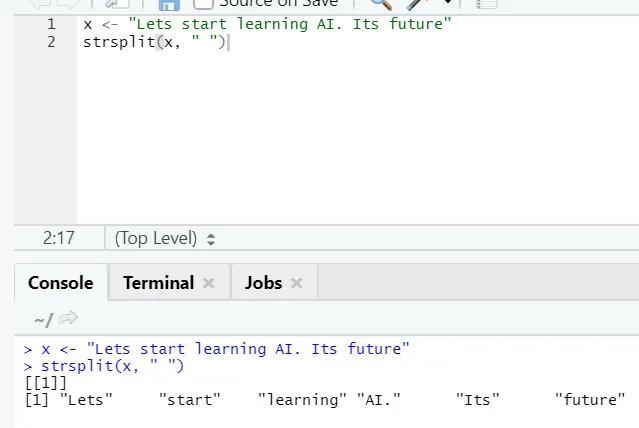
h) Rbind: Funksjonen rbind hjelper med å kjemme vektorer med samme antall kolonner, over hverandre.
Eksempel
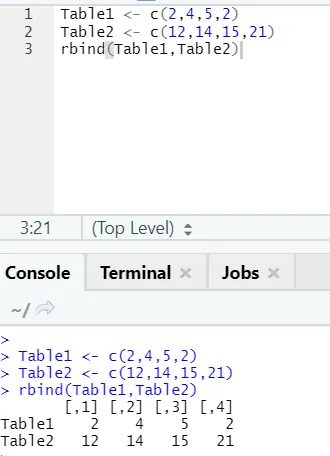
i) cbind: Dette kombinerer vektorer med samme antall rader, side om side.
Eksempel
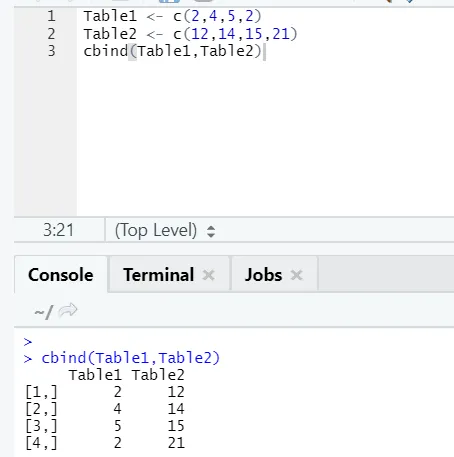
I tilfelle antall rader ikke samsvarer, er feilen nedenfor følgende:

Både cbind og rbind hjelper i datamanipulering og omforming.
2) Matematikkfunksjon -
R gir et bredt utvalg av matematiske funksjoner. La oss se noen få av dem i detalj:
a) Sqrt: Denne funksjonen beregner kvadratroten til et tall eller en numerisk vektor.
R-kode og utgang:
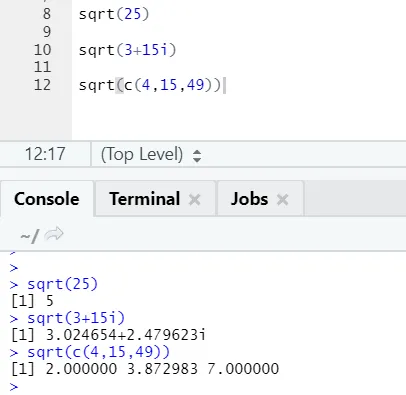
Man kan se hvordan kvadratroten av et tall, et komplekst tall og en sekvens av numerisk vektor er beregnet.
b) Exp: Denne funksjonen beregner eksponentiell verdi for et tall eller en numerisk vektor.
R-kode og utgang:
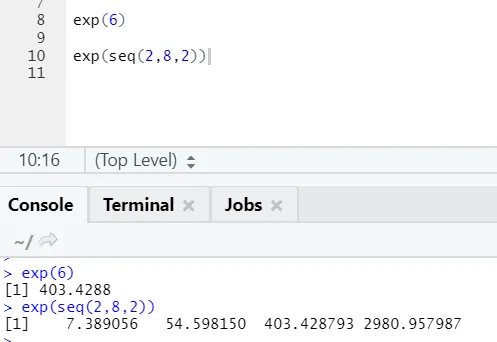
c) Cos, Sin, Tan: Dette er trigonometrifunksjoner implementert i R her.
R-kode og utgang:
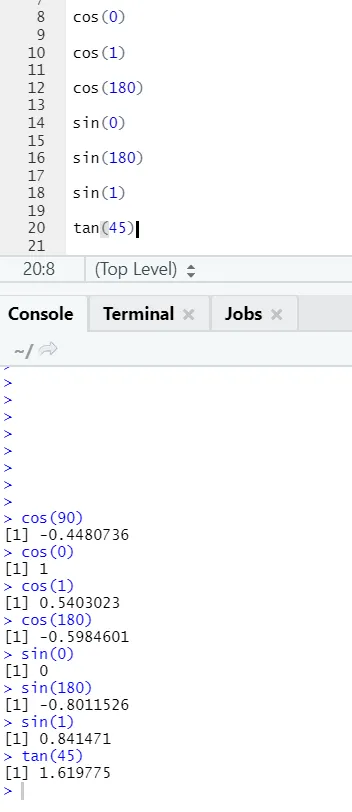
d) Abs: Denne funksjonen returnerer den absolutte positive verdien til et tall.
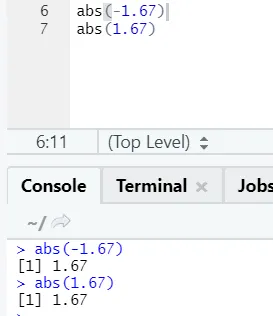
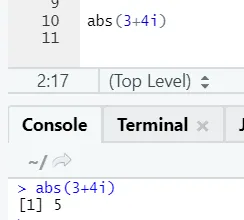
Som du ser, vil det negative eller positive av et tall returneres i sin absolutte form. La oss se det for et sammensatt antall:
e) Logg: Dette for å finne logaritmen til et nummer.
Her er eksemplet som vises nedenfor:
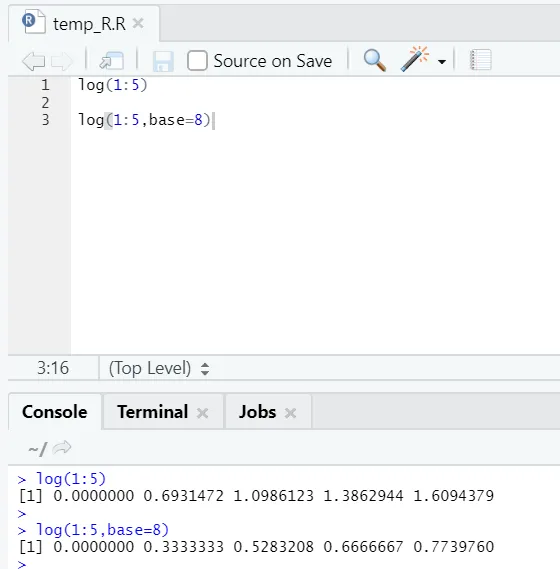
Her får man fleksibiliteten til å endre base, i henhold til krav.
f) Cumsum: Dette er en matematisk funksjon som gir kumulative summer. Her er eksemplet nedenfor:
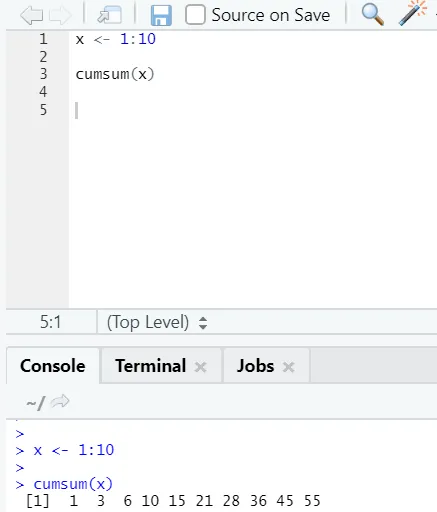
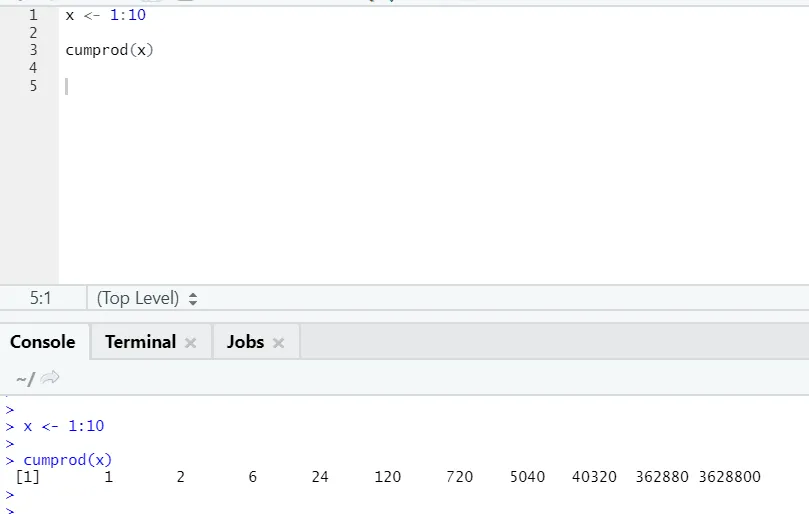
g) Cumprod: Som Cumsum matematisk funksjon, har vi cumprod der kumulativ multiplikasjon skjer.
Se eksemplet nedenfor:
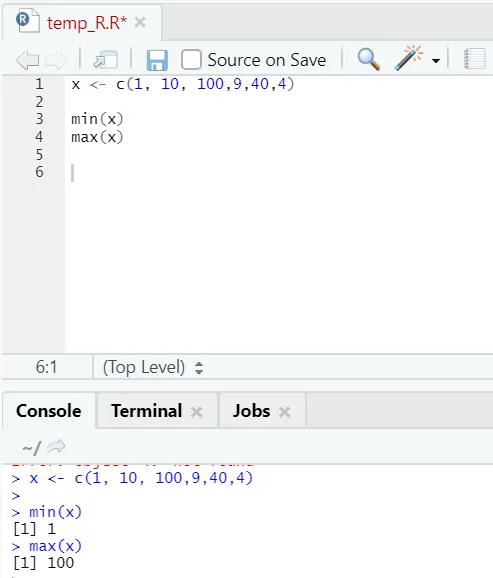
h) Max, Min: Dette hjelper deg med å finne maksimum / minimumsverdien i settet med tall. Se nedenfor eksemplene relatert til dette:
i) Tak: Taket er en matematisk funksjon som returnerer det minste av heltallet høyere enn spesifisert.
La se på et eksempel:
tak (2, 67)
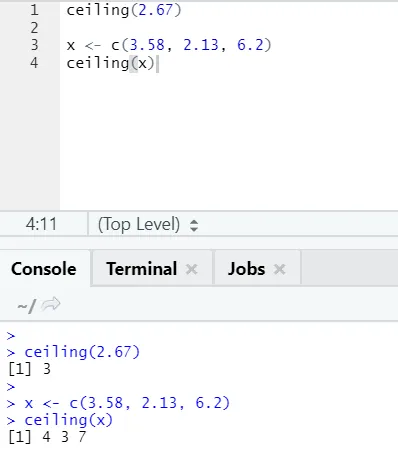
Som du kan merke, blir taket brukt over et antall så vel som over en liste, og utdataene som kommer er den minste av det neste høyere heltallet.
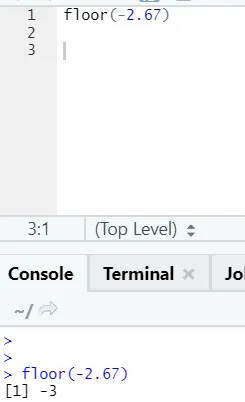
j) Gulv: Gulvet er en matematisk funksjon som returnerer det minste verdien av hele tallet for det angitte tallet.
Eksemplet nedenfor vil hjelpe deg med å forstå det bedre:
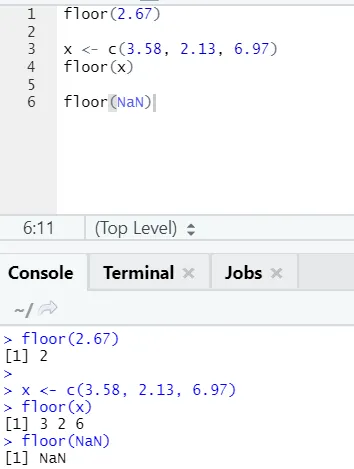
Det fungerer på samme måte for negative verdier også. Vennligst ta en titt:
3) Statistiske funksjoner -
Dette er funksjonene som beskriver den relaterte sannsynlighetsfordelingen.
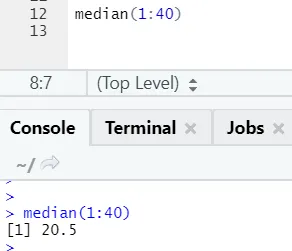
a) Median: Dette beregnet medianen ut fra tallsekvensen.
syntax
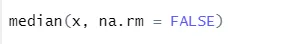
R-kode og utgang:
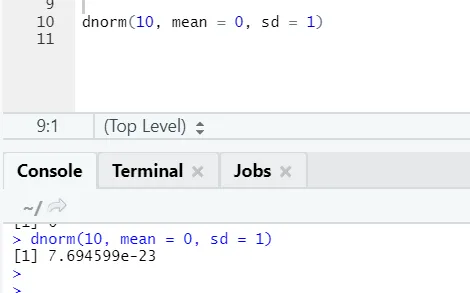
b) Dnorm: Dette refererer til normalfordeling. Funksjonen dnorm returnerer verdien av sannsynlighetstetthetsfunksjonen, for normalfordelingen gitt parametere for x, μ og σ.
R-kode og utgang:
c) Cov: Covariance forteller om to vektorer er positivt, negativt eller helt ikke-relatert.
R-kode
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
R-utgang:
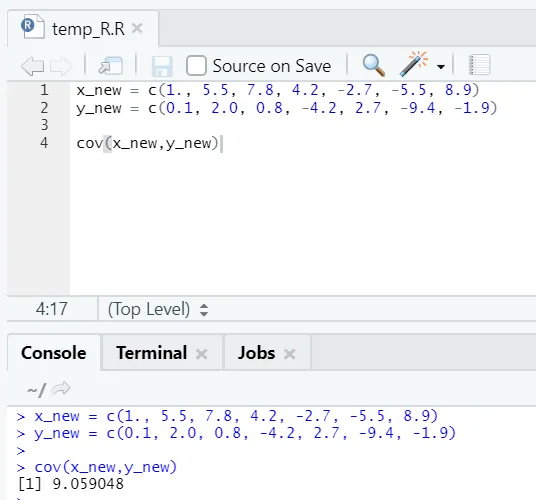
Som du kan se er to vektorer positivt relatert, noe som betyr at begge vektorene beveger seg i samme retning. Hvis samvariasjonen er negativ, betyr det at x og y er omvendt relatert og beveger seg derfor i motsatt retning.
d) Cor: Dette er en funksjon for å finne sammenhengen mellom vektorer. Det gir faktisk assosiasjonsfaktoren mellom de to vektorene som er kjent som "korrelasjonskoeffisienten". Korrelasjon tilfører en gradfaktor over samvariasjon. Hvis to vektorer er positivt korrelert, vil korrelasjonen også fortelle deg hvor mye utvide de er positivt relatert.
Disse tre typene metoder som kan brukes for å finne en sammenheng mellom to vektorer:
- Pearson korrelasjon
- Kendall korrelasjon
- Spearman korrelasjon
I enkelt R-format ser det ut som:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Her er x og y vektorer.
La oss se det praktiske eksemplet på korrelasjon over et innebygd datasett.
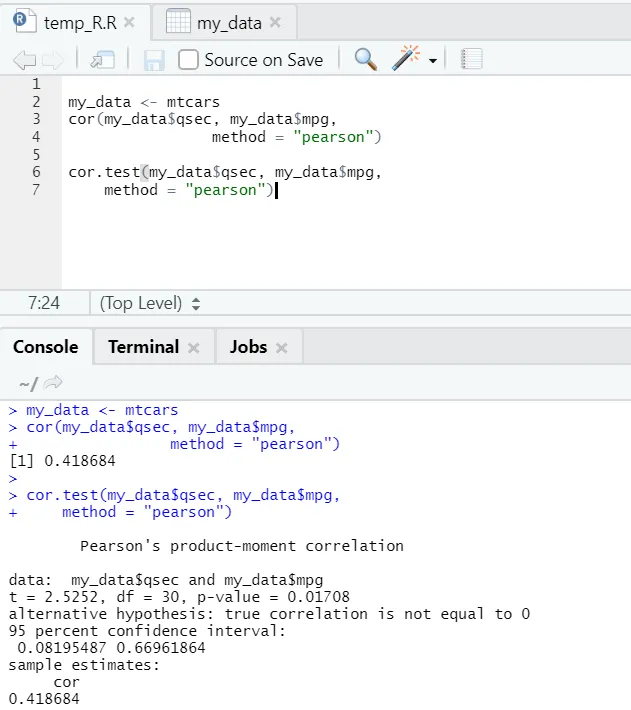
Så her kan du se “cor ()” -funksjonen ga korrelasjonskoeffisienten 0, 41 mellom “qsec” og “mpg”. Imidlertid har en funksjon også blitt vist frem, dvs. "cor.test ()", som ikke bare forteller korrelasjonskoeffisienten, men også p-verdien og t-verdien relatert til den. Tolkning blir langt enklere med cor.test-funksjon.
Tilsvarende kan gjøres med de to andre korrelasjonsmetodene:
R-kode for Pearson-metoden:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
R-kode for Kendall-metoden:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
R-kode for Spearman-metoden:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Korrelasjonskoeffisienten varierer mellom -1 og 1.
Hvis korrelasjonskoeffisienten er negativ, vil det si at x øker y.
Hvis korrelasjonskoeffisienten er null, betyr det at det ikke er noen sammenheng mellom x og y.
Hvis korrelasjonskoeffisienten er positiv, betyr det at x øker y, har også en tendens til å øke.
e) T-test: T-testen vil fortelle deg om to datasett kommer fra samme (forutsatt) normale distribusjoner eller ikke.
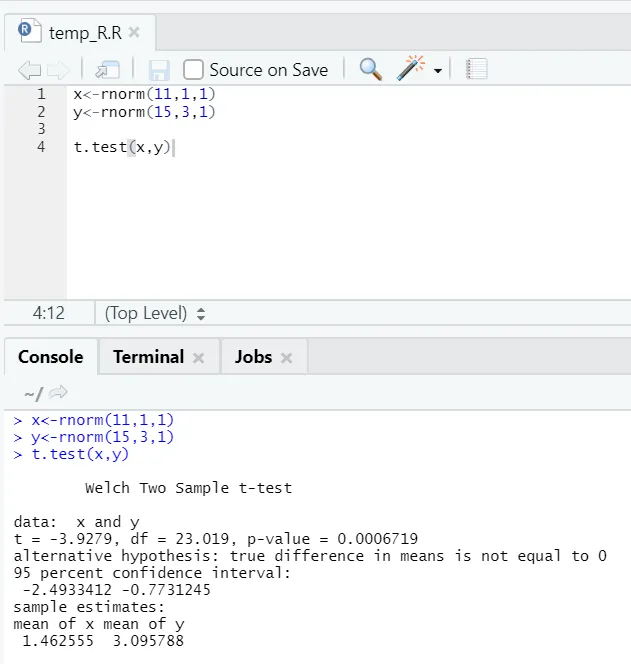
Her bør du avvise nullhypotesen om at de to midlene er like fordi p-verdien er mindre enn 0, 05.
Denne viste forekomsten er av typen: uparede datasett med ulik avvik. Tilsvarende kan du prøve med det sammenkoblede datasettet.
f) Enkel lineær regresjon: Dette viser forholdet mellom prediktoren / uavhengig og respons / avhengig variabel.
Et enkelt praktisk eksempel kan være å forutsi vekten til en person hvis høyden er kjent.
R syntaks
lm(formula, data)
Her viser formelen forholdet mellom output dvs. y og input variabel iex Data representerer datasettet, som formelen må brukes på.
La oss se et praktisk eksempel, der gulvområdet er inngangsvariabelen og leie er utgangsvariabelen.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
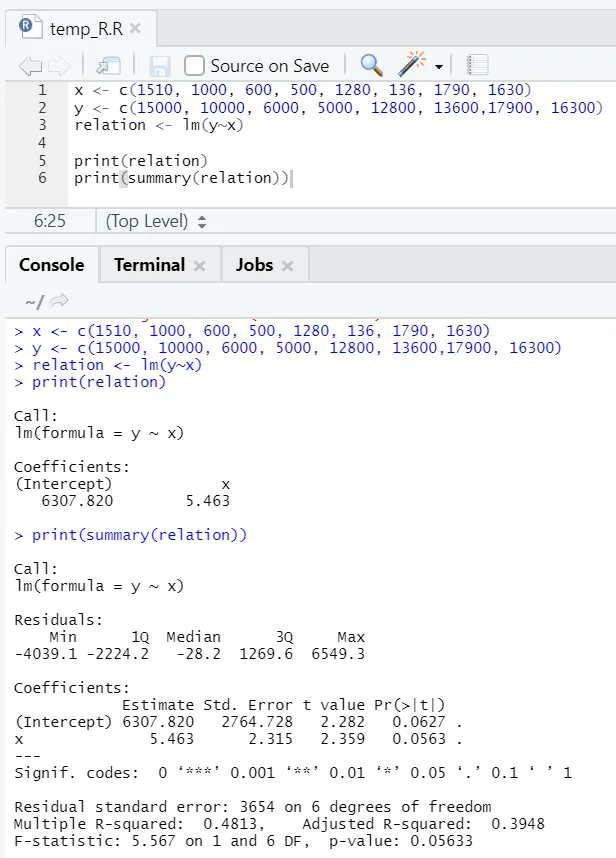
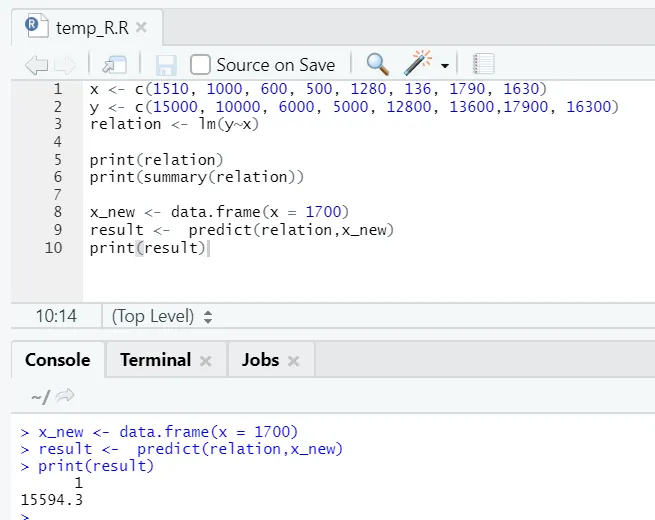
Her er P-verdien ikke mindre enn 5%. Nullhypotesen kan derfor ikke avvises. Det er ikke så stor betydning å bevise forholdet mellom gulvareal og leie.
Her er R-kvadratverdien 0, 4813. Det innebærer at bare 48% av variansen i utgangsvariabelen kan forklares med inputvariabelen.
La oss si at nå må vi forutsi verdien av gulvarealet, basert på den ovennevnte modellen.
R-kode
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
R-utgang:
Etter utførelsen av R-koden ovenfor, vil utdataen se slik ut:
Man kan passe og visualisere regresjon. Her er R-koden for det:
# Gi png-kartfilen et navn.
png(file = "LinearRegressionSample.png.webp")
# Plott diagrammet.
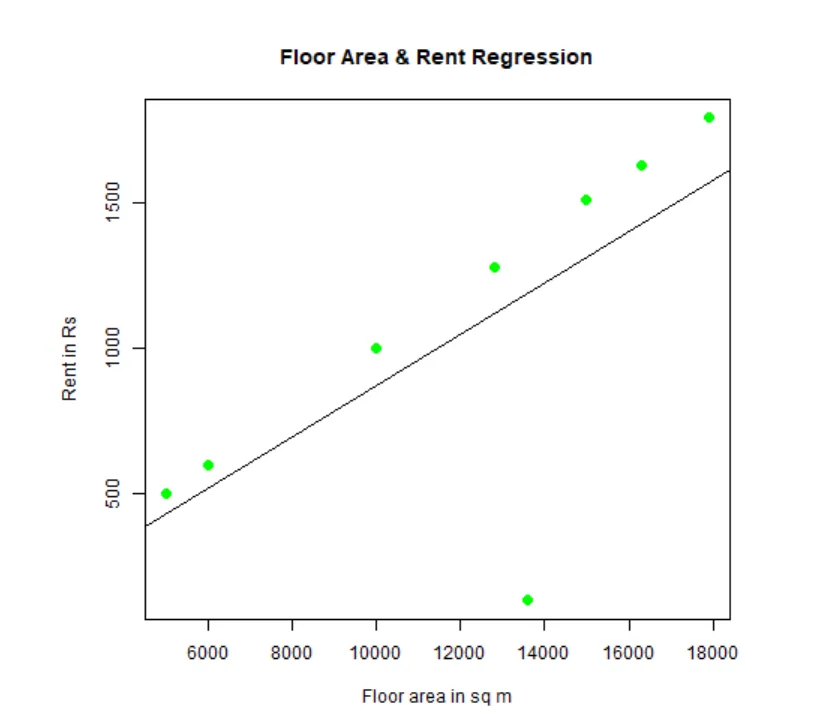
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Lagre filen.
dev.off()
Denne "LinearRegressionSample.png.webp" grafen vil bli generert i din nåværende arbeidskatalog.
g) Chi-Square-test
Dette er en statistisk funksjon i R. Denne testen har sin betydning for å bevise om korrelasjonen eksisterer mellom to kategoriske variabler.
Denne testen fungerer også som alle andre statistiske tester var basert på p-verdi, man kan godta eller avvise nullhypotesen.
R syntaks
chisq.test(data), /code>
La oss se et praktisk eksempel på det.
R-kode
# Last inn biblioteket.
library(datasets)
data(iris)
# Lag en dataramme fra hoveddatasettet.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Lag en tabell med de nødvendige variablene.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Utfør Chi-Square-testen.
print(chisq.test(iris.data))
R-utgang:
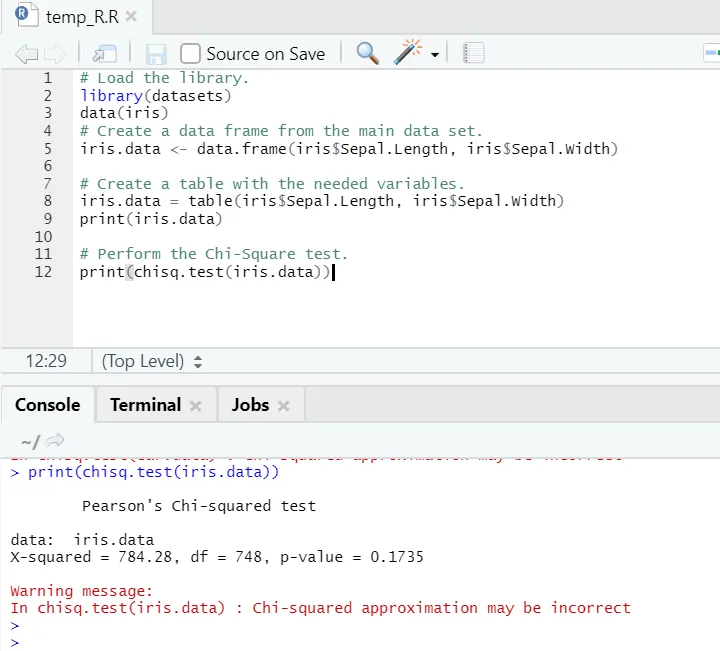
Som man kan se, har chi-square-testen blitt utført over et iris-datasett, med tanke på de to variablene “Sepal. Lengde ”og“ Sepal.Width ”.
P-verdien er ikke mindre enn 0, 05, og derfor eksisterer det ikke korrelasjon mellom disse to variablene. Eller vi kan si at disse to variablene ikke er avhengige av hverandre.
Konklusjon
Funksjoner i R er enkle, enkle å passe, enkle å forstå og likevel veldig kraftige. Vi så en rekke funksjoner som brukes som en del av det grunnleggende i R. Når man blir komfortabel med disse funksjonene omtalt ovenfor, kan man utforske andre varianter av funksjoner. Funksjoner hjelper deg å gjøre koden din kjørt på en enkel og konsis måte. Funksjoner kan være innebygd eller brukerdefinert, alt avhenger av behovet mens du løser et problem. Funksjoner gir en god form til et program.
Anbefalte artikler
Dette er en guide til Funksjoner i R. her diskuterer vi hvordan du skriver Funksjoner i R og forskjellige typer funksjoner i R med syntaks og eksempler. Du kan også se på følgende artikkel for å lære mer -
- R strengfunksjoner
- SQL-strengfunksjoner
- T-SQL-strengfunksjoner
- PostgreSQL strengfunksjoner