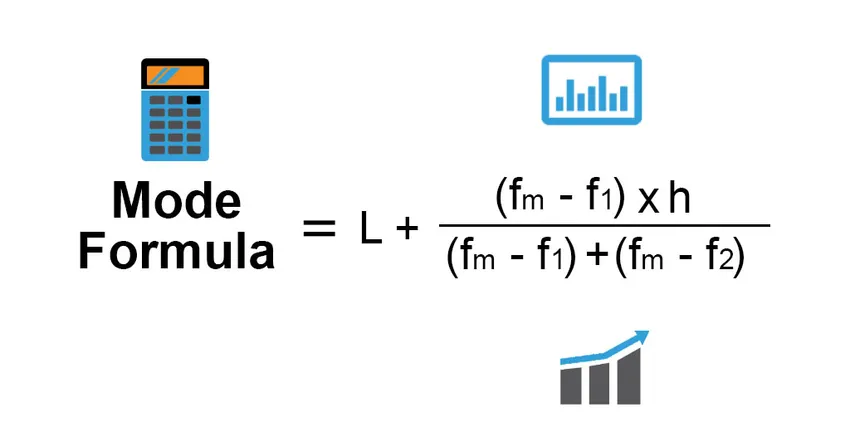
Modusformel (innholdsfortegnelse)
- Formel
- eksempler
- Kalkulator
Hva er modusformelen?
De tre sentrale tendensmålene er gjennomsnittlig median og modus. Når alle tre brukes sammen for å trekke ut meningsfull analyse i datasettet. I dag i denne artikkelen vil vi diskutere modus som også er en av tastene og den viktige metoden sentrale tendensen som brukes. Mode refererer til den hyppigst forekommende verdien i datasettet. Modus for en data kan bli funnet med normalt datasett, gruppedatasett så vel som ikke-gruppert eller ugruppert datasett. Imidlertid forblir middelet som er mest brukt fortsatt det beste målet på sentral tendens til tross for eksistensen av middel, median og modus. I denne artikkelen vil vi prøve å forstå modusfunksjonen, eksempler og forklaringer på hvert eksempel sammen med formelen og beregningene.
Formelen for modus er: -
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
Modusformel for grupperte data:
Mode = L + (fm − f1) h / 2fm − f1 − f2
Hvor,
- L = Nedre grense Modus for modalklasse
- fm = Frekvens av modalklasse
- f1 = Frekvens av klasse som går foran modalklassen
- f2 = Frekvens av klasse som etterfølger modalklassen
- h = Størrelse på klassens intervall
Eksempler på modusformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av modus på en bedre måte.
Du kan laste ned denne Mode Formula Excel Template her - Mode Formula Excel TemplateModusformel - eksempel # 1
Hvor modus beregnes ganske enkelt antall observasjoner i et datasett som forekommer mesteparten av tiden.
Beregn modus for følgende datasett.
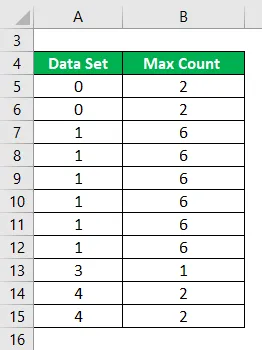
Løsning:
En modus beregnes som:
Antall observasjoner i et datasett som forekommer mesteparten av tiden
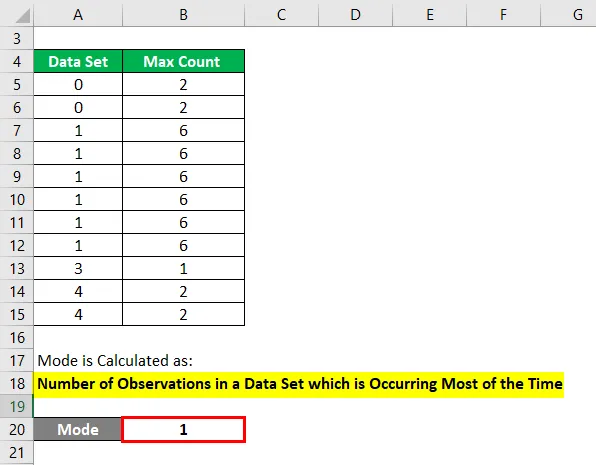
- Mode = 1
Modusformel - eksempel # 2
Beregn modus ved å bruke den gitte informasjonen.
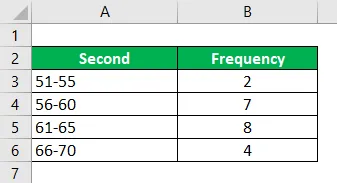
Løsning:
Merk: - Først må modalgruppen med høyest frekvens for å identifisere Hvis intervallet ikke er kontinuerlig, skal 0, 5 trekkes fra nedre grense-modus og 0, 5 bør legges til fra øvre grense-modus. Da blir intervallet
Modal Group beregnes som:
Modal gruppe som er hyppigst, dvs. 60, 5-65, 5
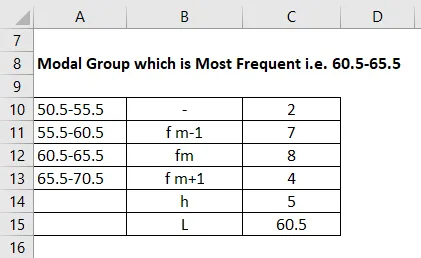
Da er den lavere frekvensen av den modale gruppen som er 4, i dette tilfellet blir tatt som fm + 1 og fm-1 vil bli 7 i dette eksemplet. Og vi har fm som er frekvensen som 8. Den (h) kalles størrelsen på klassens intervall er 5 som vi også vurderer startintervallet. L er 60, 5.
Modusen beregnes ved å bruke formelen nedenfor
Mode = L + (fm − f1) h / (fm − f1) + (fm − f2)
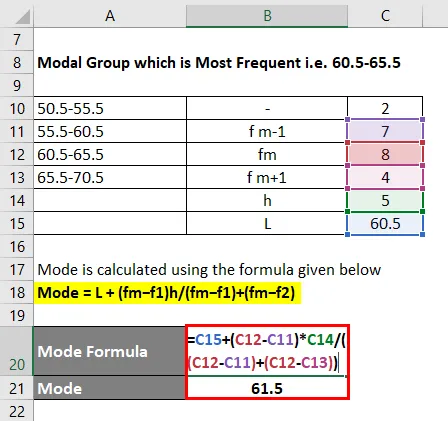
- Mode = 60, 5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
- Mode = 61, 5
Modusformel - eksempel # 3
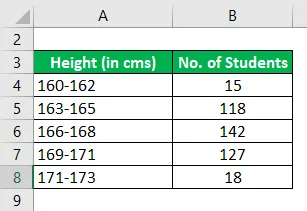
Følgende er høydefordelingen i en viss klasse av elever i en viss modus
Beregn modus ved å bruke den gitte informasjonen.
Løsning:
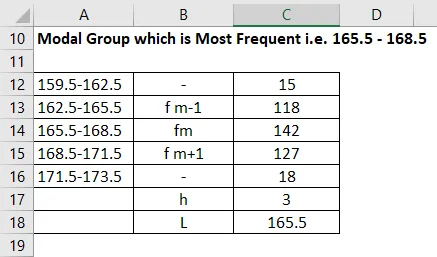
Hvis intervallet ikke er kontinuerlig, skal 0, 5 trekkes fra modus for nedre grense og 0, 5 legges til fra øvre grense-modus. Da blir intervallet
Modal Group beregnes som:
Modal gruppe som er hyppigst, dvs. 165, 5-168, 5
Modusen beregnes ved å bruke formelen gitt nedenfor
Mode = L + (fm − f1) h / (fm − f1) + (fm − f2)
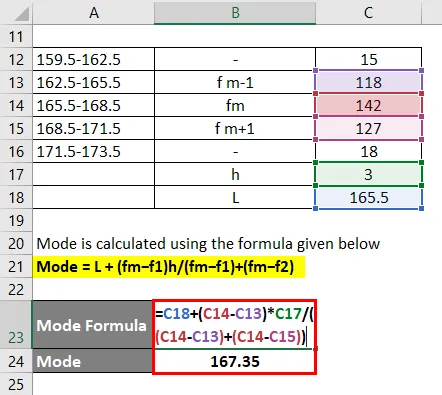
- Mode = 165, 5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
- Mode = 167, 35
Forklaring
Modusen kan enkelt forklares som den verdien som hyppigst forekommer i datasettet. Og modusen over kan forklares som når data er en gruppe vi først må beregne modalfunksjonen og også gjøre dataene kontinuerlige for å beregne modus for dataene. Modalklassen avgjøres med klassen som har den høyeste frekvensen i datasettet.
Relevans og bruk av formel
- Gjennomsnitt, median og modus avslører forskjellige aspekter av dataene dine. Alle vil gi deg en generell ide, men kan villede deg; å ha alle tre vil gi deg et mer fullstendig bilde
- For en normalfordeling har modus, gjennomsnitt, median samme verdi siden Mode er en normalfordeling. Analysemodus isolert gjenspeiler ikke det sanne bildet, hvis du vil analysere det komplette datasettet, bør alle de tre statistiske målene analyseres i detalj og tolkes
- Modusen er lett å forstå og enkel å beregne.
- Modusen påvirkes ikke av ekstremt store eller små verdier.
- Modusen kan lokaliseres bare ved inspeksjon i ugrupperte data og diskret frekvensfordeling.
- Modusen kan være nyttig for kvalitative data.
- Modusen kan beregnes i en åpen frekvens tabell.
- Modusen kan plasseres grafisk
- Modus brukes ofte av dataforskere
- Modus er at det ikke vil gi oss et veldig godt mål på sentral tendens når det vanligste merket er langt borte fra resten av dataene i datasettet
Mode Formula Calculator
Du kan bruke følgende modulformuleringskalkulator
| L | |
| fm | |
| f1 | |
| f2 | |
| h | |
| Modusformel | |
| Modusformel = | L + (fm - f1) xh / (fm - f1) + (fm - f2) |
| = | 0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0 |
Anbefalte artikler
Dette er en guide til Mode Formula. Her diskuterer vi hvordan du beregner Mode Formula sammen med praktiske eksempler. Vi tilbyr også en modus-kalkulator med en nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Eksempler på Gordon Growth Model Formula
- Formel for beregning av kapitalandelsprisingsmodell
- Kalkulator for formel for total kostnadsforhold
- Poisson distribusjonsformel (eksempler med Excel-mal)