Excel NORMSINV (Innholdsfortegnelse)
- Introduksjon til Excel NORMSINV
- Hvordan bruke NORMSINV-formelen i Excel?
Introduksjon til Excel NORMSINV
Invers normal kumulativ fordelingsfunksjon i excel er et viktig verktøy som returnerer invers normal kumulativ fordeling for en gitt sannsynlighetsverdi, dvs. den returnerer normalt inverse av standard normal kumulativ fordeling (som har et gjennomsnitt på null og et standardavvik på en) NORM.S.INV-funksjonen ble først introdusert i Microsoft Excel-versjon 2010, som er en oppdatert versjon av NORMSINV-funksjonen i Excel 2013 og den nyeste versjonen. NORMSINV-funksjonen brukes mest i leverandørgjeld og finansanalyse.
Syntaks for Excel NORMSINV

Argument:
Sannsynlighet - Som ikke er annet enn sannsynlighet tilsvarer normalfordelingen.
Hvordan bruke NORMSINV-formelen i Excel?
I Microsoft Excel er NORMSINV innebygde funksjon kategorisert under statistisk funksjon som vises i skjermbildet nedenfor (hvor den vil beregne inverse av normal kumulativ distribusjon for en gitt sannsynlighet).
- Gå til formelmeny.
- Klikk på More Function som vist på skjermbildet nedenfor.

- Velg en statistisk kategori under at vi finner NORM.DIST-funksjonen som vist nedenfor.
Eksempel 1 - Bruke NORM.DIST og NORMSINV
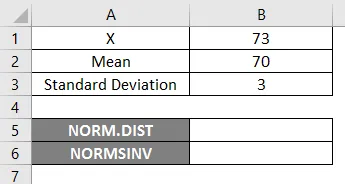
For å bruke NORM.DIST-funksjonen, la oss starte med et enkelt eksempel der vi trenger å finne ut studentkarakterene, antar at vi har klasseeksamen med gjennomsnittlig karakter 70 dvs. mu = 70 og klassens standardavvik er 3 poeng dvs. sigma = 3 her må vi finne ut hva som er sannsynligheten for at studentene fikk karakterene 73 eller under dvs. P (X <= 73). Så la oss se hvordan du finner ut sannsynligheten ved å bruke NORM.DIST-funksjonen.
- X = 3-
- Mean = 70
- Standardavvik = 3
- Bruk NORM.DIST-funksjonen som nedenfor.
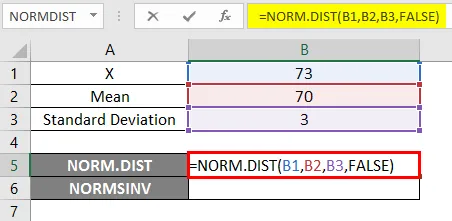
- Hvis vi bruker funksjonen NORM.DIST ovenfor, vil vi få sannsynligheten til 0, 0807.
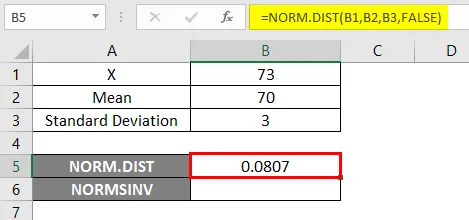
- Bruk nå NORMSINV-funksjonen for å finne ut omvendt av den normale kumulative fordelingen som vist nedenfor.
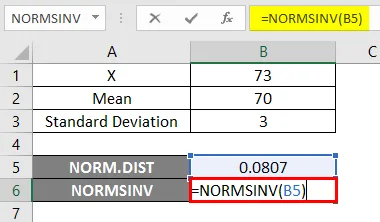
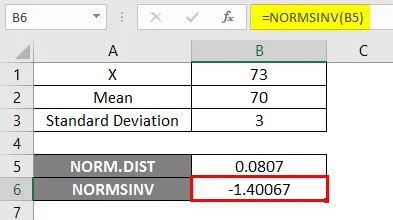
Resultat -
I resultatet nedenfor kan vi se at vi fikk negative verdier -1.40067 for den gitte sannsynligheten, dvs. invers av normal kumulativ fordeling.
Eksempel 2 - Gjennomsnittlig og eksakt standardavvik
La oss se et annet eksempel med kurvebaserte data slik at vi kan bli kjent med gjennomsnittet og eksakt standardavvik.
- Gjennomsnitt = 7
- Standardavvik = 1.3
- Standardavviksøkning som -3

- For å få klokkekurven må vi legge til 0, 1 til standardavviksøkning der dataene er som vist nedenfor.
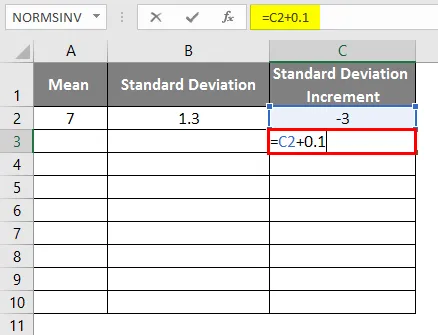
- Etter anvendelse av formelen er resultatet som vist nedenfor.
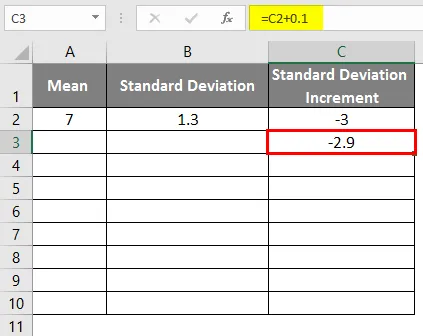
- Dra verdiene for å få flere verdier til vi får de positive verdiene slik at vi får en venstre kurve.
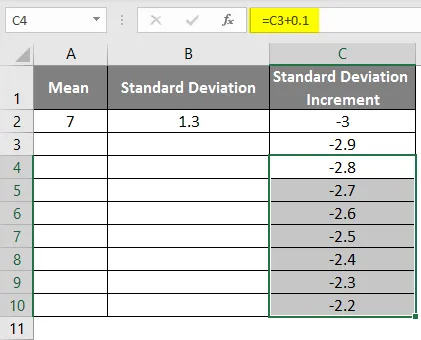
- For å få riktig kurve må vi bruke formelen som = gjennomsnittlig standardavvik * 3 slik at vi får de nøyaktige kurvene.
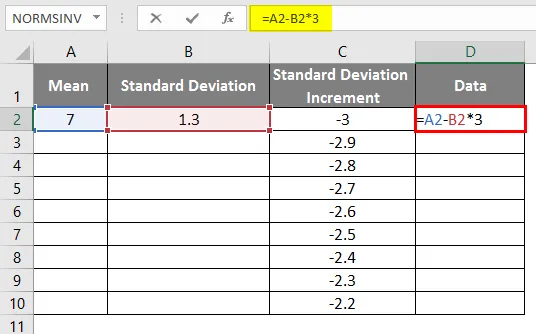
- Etter bruk av formelen vises resultatet nedenfor.
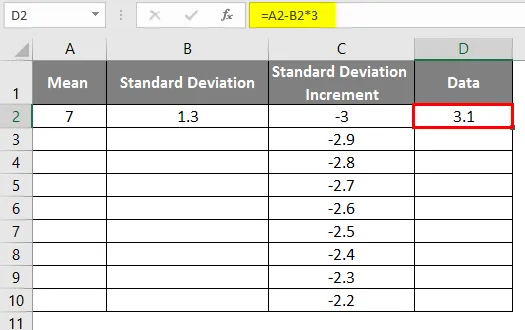
- Som i dataene ovenfor for standardavviksøkning for å få venstre kurve, har vi økt verdiene med 0, 1
- Det samme scenariet brukes ved å bruke formelen som = 3.1 + STANDARD DEVIATION / 10 for å få kurveøkningen 0.1
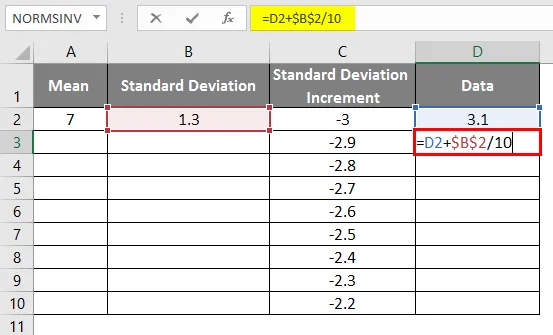
- Etter bruk av formelen vises resultatet nedenfor.

- Dra verdiene for å få det eksakte resultatet som vises i skjermbildet nedenfor.
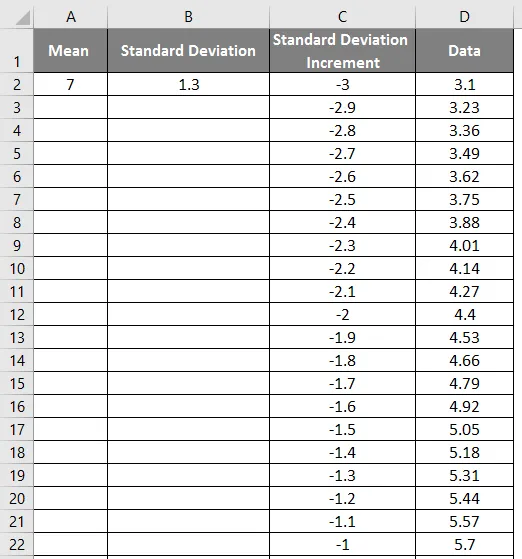
- Bruk nå normalfordelingsfunksjonen med formelen = NORM.DIST (DATA-verdi, middel, standardavvik, usant).
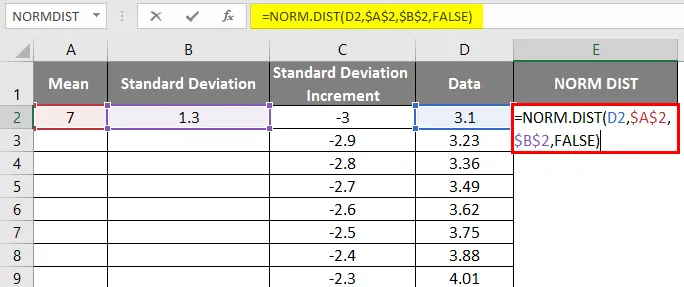
- Vi får resultatet nedenfor som følger.
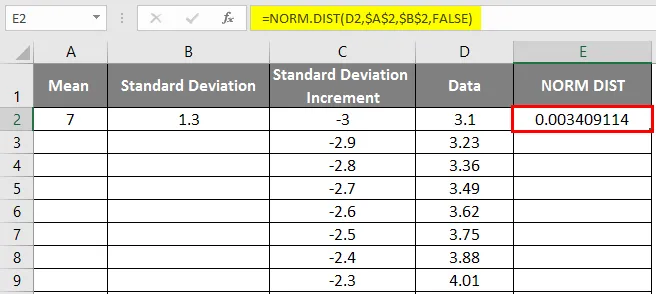
- Dra verdiene for å få det eksakte resultatet som vises nedenfor.
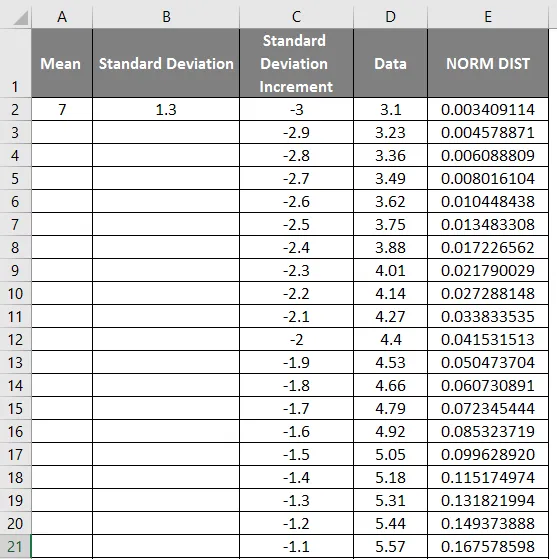
- Som vi kan se på skjermbildet ovenfor, har vi beregnet NORMAL distribusjon fra middel- og standardavviket. La oss se hva som vil være det inverse av NORMAL distribusjon ved å bruke NORMSINV som er vist nedenfor.
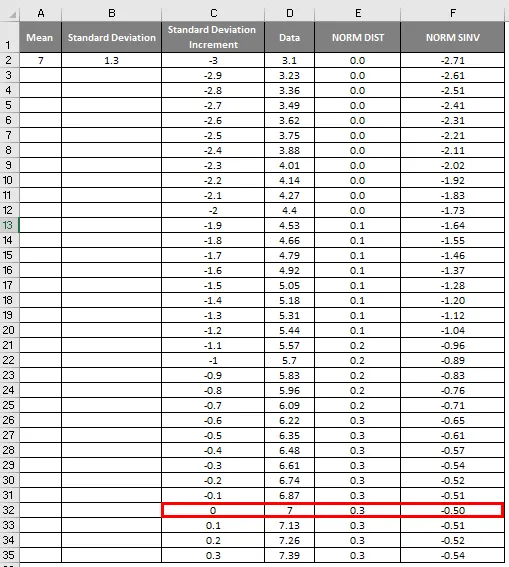
- Her kan vi se at Value Zero (0) har et standardavvik som 7.

Bruk spredt graf for å se på hvordan venstre og høyre kurve ser ut.
- Velg først dataene og kolonnen Normal.
- Gå til kategorien Sett inn og velg den spredte grafen som følger.
- Vi får kurven nedenfor som vist nedenfor.
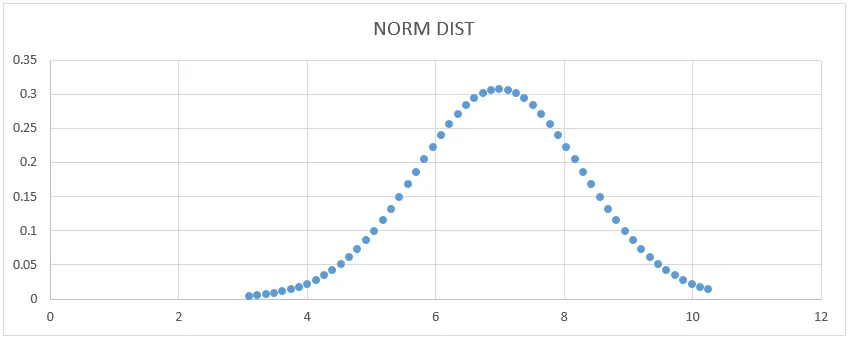
Her kan vi se at middelverdien 7 har en standardavviksform der vi kan vise det ved å tegne en rett linje for å representere den.
- Gjennomsnitt = 7
- 1 –Standardavvik indikerer 68% av data.
- 2 –Standardavvik indikerer 95% av data.
- 3 –Standardavvik indikerer 99, 7% av data.
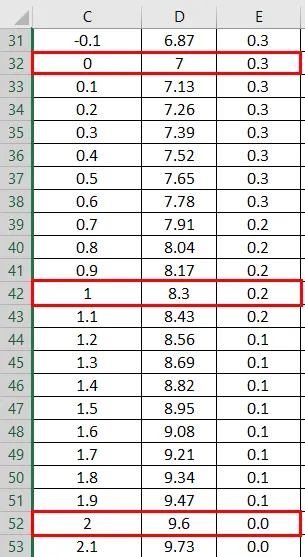
Normal distribusjonsgraf:
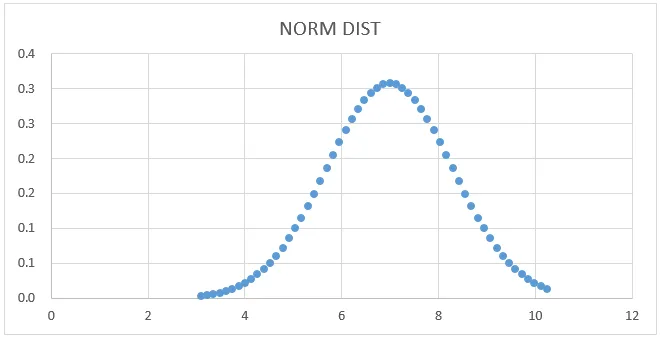
NORMSINV Graf:
Fra figuren over velger du datakolonnen og NORM SINV for å få grafen nedenfor som følger.
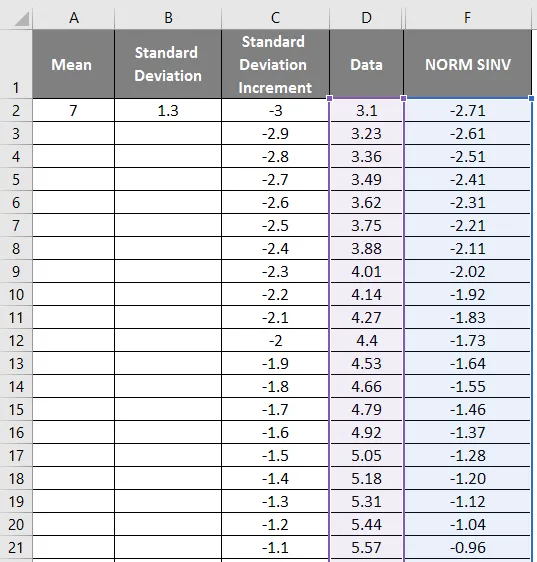
- Velg først dataene og kolonnen Normal.
- Gå til kategorien Sett inn og velg den spredte grafen.
- Vi får grafen nedenfor som vises på skjermbildet nedenfor.
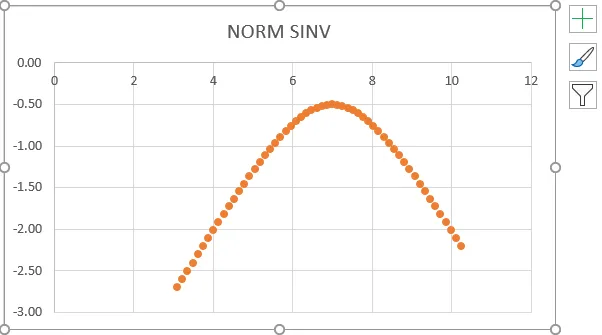
- Fra skjermbildet over kan vi se at vi fikk en nøyaktig invers av en normalfordeling som viser den samme verdifiguren som er vist nedenfor.

Eksempel 3 - Konfigurering av venstre og høyre kurve
I dette eksemplet vil vi konfigurere venstre og høyre kurve ved hjelp av normal distribusjonsfunksjon. Tenk på dataene nedenfor som vist nedenfor der x har negativverdier og blir økt til positive verdier.
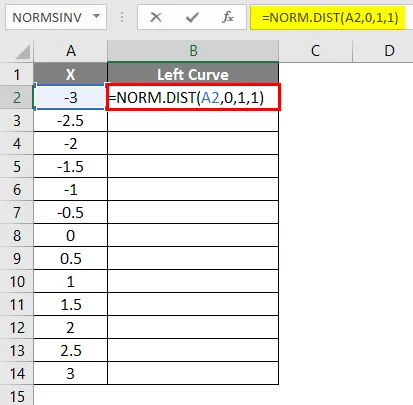
- Bruk formelen = NORM.DIST (A2, 0, 1, 1).
- Etter anvendelse av formelen vises resultatet nedenfor.
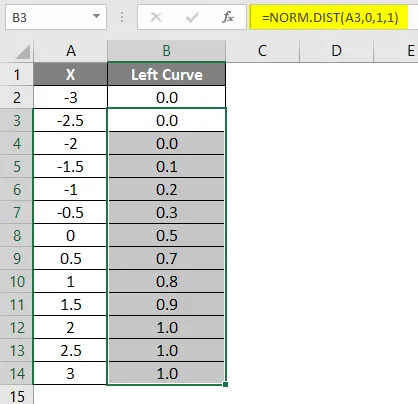
- Dra formelen i andre celler.
- Bruk formel = 1-B2 .
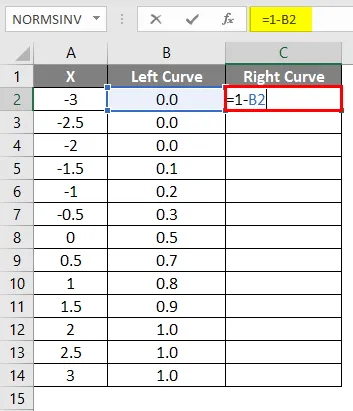
- Etter bruk av formel vises resultatet nedenfor.
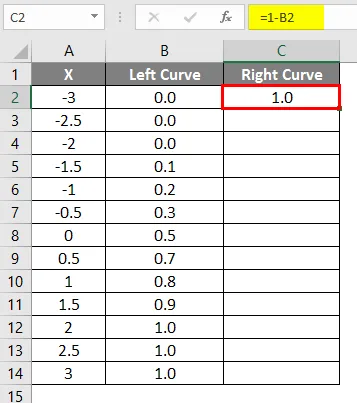
- Dra den samme formelen i andre celler.
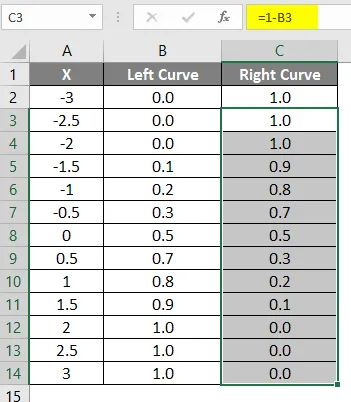
Resultatet av den ovenfor anvendte formelen er vist nedenfor.
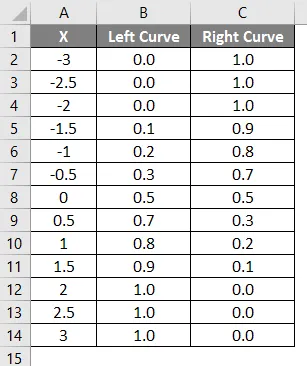
- Verdiene for venstre kurve er beregnet ved å bruke NORMAL DISTRIBUTION-formelen ved å sette den kumulative verdien som True, og NORMSINV er beregnet ved å bruke venstre kurve.
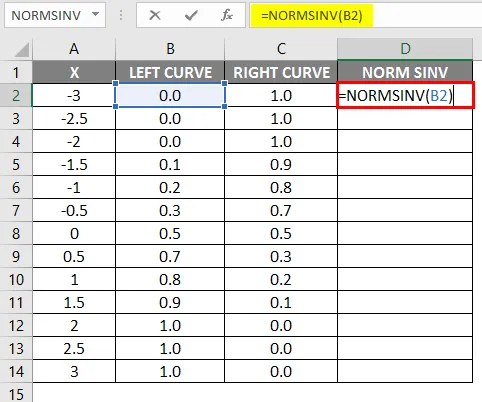
- Etter anvendelse av formelen vises resultatet nedenfor.
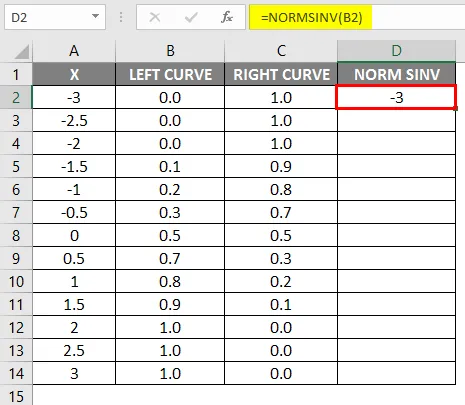
- Dra den samme formelen i andre celler.
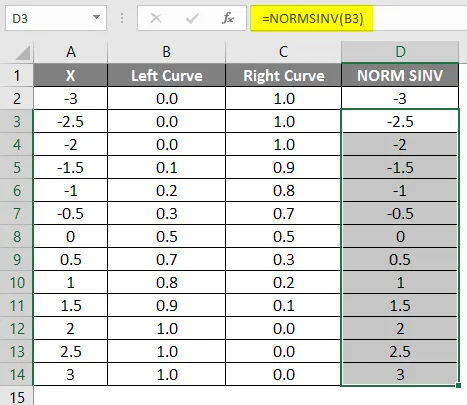
Som vi kan se at vi fikk den samme verdien for NORMSINV som ikke er noe annet enn den inverse av normalfordelingen. På samme måte vil vi få riktig kurveverdi ved å beregne 1-venstre kurveverdi. I neste trinn skal vi sjekke hvordan vi får høyden på x ved å bruke den spredte grafen.
- Velg venstre kur og kolonne til høyre kurve.
- Gå til å sette inn meny.
- Velg den spredte grafen som følger.
Vi får resultatet under grafen som vist nedenfor.
NORM SINV Graf:
I grafen under kan vi se at NORM DISTRIBUTION verdi venstre kurve har den eksakte samsvar for (0, 0.5) som ligger i midten av linjen hvor vi vil få den samme grafen hvis vi søker om NORMDIST.
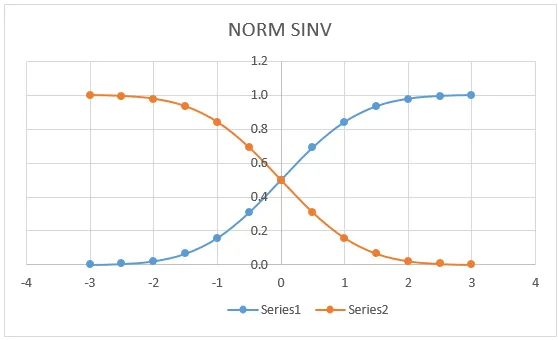
Her i grafen over viser det veldig tydelig at vi fikk den eksakte middelverdien på et midtpunkt som angir:
- X = 0
- Venstre kurve = 0, 5
- Høyre kurve = 0, 5
Vi viste den for å vise NORMSINV-verdiene i et grafisk format som vist nedenfor.
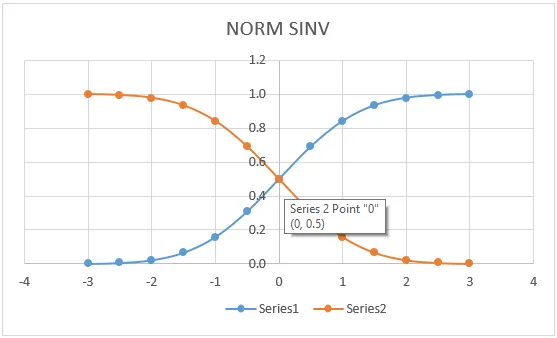
Ting å huske på om Excel NORMSINV
- #verdi! Feil oppstår når det gitte argumentet er ikke-numerisk eller logisk verdi.
- I Normal distribusjonsfunksjon får vi vanligvis #NUM! feil på grunn av standardavviksargumentet er mindre enn eller lik null.
Anbefalte artikler
Dette er en guide til Excel NORMSINV. Her diskuterer vi hvordan du bruker NORMSINV i Excel sammen med praktiske eksempler og nedlastbar Excel-mal. Du kan også gå gjennom andre foreslåtte artikler -
- Hvordan bruker jeg navneboks i Excel?
- Jobber med Matrix i Excel
- Hva om analyse i Excel
- NPV-formel i Excel