
Poisson distribusjonsformel (innholdsfortegnelse)
- Formel
- eksempler
- Kalkulator
Hva er Poisson distribusjonsformel?
I Probability and Statistics er det tre typer distribusjoner basert på kontinuerlige og diskrete data - Normal, Binomial og Poisson Distribusjoner. Normal distribusjon er ofte som en bjellekurve. Poisson-distribusjon ofte referert til som Distribusjon av sjeldne hendelser. Dette brukes hovedsakelig for å forutsi sannsynligheten for hendelser som vil oppstå basert på hvor ofte hendelsen hadde skjedd i fortiden. Det gir muligheten for at et gitt antall hendelser vil oppstå i et sett av perioden. Det brukes i mange virkelige situasjoner.
Formel for å finne Poisson-distribusjon er gitt nedenfor:
P(x) = (e -λ * λ x) / x!
For x = 0, 1, 2, 3 …
Dette eksperimentet teller generelt antall hendelser som skjedde i området, avstand eller volum. Sammen med dette kan man finne hendelseskjeden som ikke er annet enn kjeden av forekomster av den samme hendelsen over den bestemte tidsperioden. Poisson-distribusjonen har følgende felles egenskaper.
- En hendelse kan skje når som helst når som helst.
- Arrangementet kan vurdere alle tiltak som volum, område, avstand og tid.
- Imidlertid er sannsynligheten for at en hendelse skal skje i alle tiltak som er spesifisert over, den samme.
- Hver hendelse er ikke avhengig av alle andre hendelser som betyr at sannsynligheten for at en hendelse ikke skal påvirke andre hendelser som skjer samtidig.
Eksempler på Poisson distribusjonsformel
La oss ta et eksempel for å forstå beregningen av Poisson-distribusjonen på en bedre måte.
Du kan laste ned denne Poisson Distribution Formula Excel Template her - Poisson Distribution Formula Excel TemplatePoisson distribusjonsformel - eksempel # 1
Gjennomsnittlig antall årlige ulykker skjer på en jernbanestasjon under togbevegelsen er 7. For å identifisere sannsynligheten for at det er nøyaktig 4 hendelser på samme plattform i år, kan Poisson distribusjonsformel brukes.
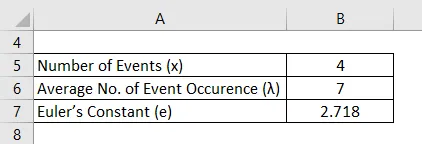
Løsning:
Poisson Distribusjon beregnes ved å bruke formelen gitt nedenfor
P (x) = (e -λ * λ x) / x!
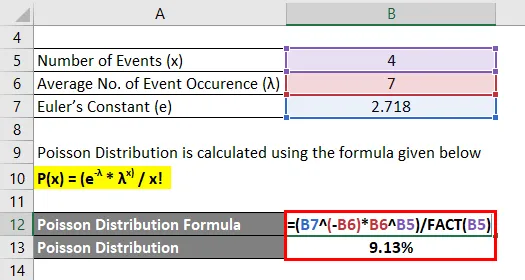
- P (4) = (2, 718 -7 * 7 4) / 4!
- P (4) = 9, 13%
For det gitte eksempelet er det 9, 13% sjanse for at det vil være nøyaktig samme antall ulykker som kan skje i år.
Poisson distribusjonsformel - eksempel # 2
Antall skrivefeil gjort av en maskinskriver har en Poisson-distribusjon. Feilene gjøres uavhengig med en gjennomsnittlig hastighet på 2 per side. Finn sannsynligheten for at et tre sider langt brev ikke inneholder feil.
Her gjennomsnittlig rate per side = 2 og gjennomsnittlig rate for 3 sider (λ) = 6
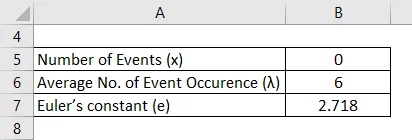
Løsning:
Poisson Distribusjon beregnes ved å bruke formelen gitt nedenfor
P (x) = (e -λ * λ x) / x!
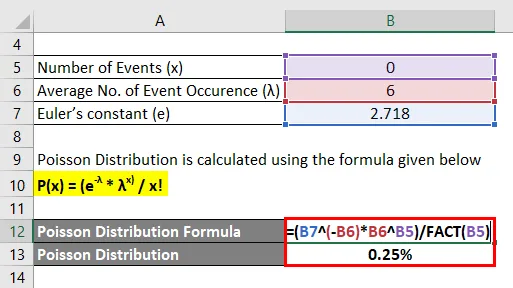
- P (0) = (2.718 -6 * 6 0 ) / 0!
- P (0) = 0, 25%
Derfor er det 0, 25% sjanse for at det ikke blir feil på 3 sider.
Merk : x 0 = 1 (hvilken som helst verdi effekt 0 vil alltid være 1) ; 0! = 1 (null faktor vil alltid være 1)Forklaring
Nedenfor er trinn for trinn for å beregne Poisson distribusjonsformelen.
Trinn 1: e er Eulers konstant som er en matematisk konstant. Generelt er verdien av e 2, 718 .
Trinn 2: X er antall faktiske hendelser som skjedde. Det kan ha verdier som følgende. x = 0, 1, 2, 3 …
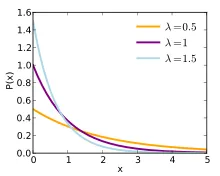
Trinn 3: λ er det gjennomsnittlige (gjennomsnittlige) antall hendelser (også kjent som “Parameter of Poisson Distribution). Hvis du tar det enkle eksemplet for beregning av λ => 1, 2, 3, 4, 5. Hvis du bruker det samme datasettet i formelen ovenfor, n = 5, derav gjennomsnitt = (1 + 2 + 3 + 4 + 5) / 5 = 3. For et stort antall data er det ikke mulig å finne median manuelt. Så det er viktig å bruke formelen for et stort antall datasett. Her ved beregning av Poisson-distribusjon vil vi vanligvis få gjennomsnittstallet direkte. Basert på verdien av λ, kan Poisson-grafen være unimodal eller bimodal som nedenfor.
Trinn 4: x! er faktoren for faktiske hendelser skjedde x. Nedenfor er et eksempel på hvordan du beregner fakultet for det gitte antallet.
Hvis du tar det enkle eksemplet for beregning av Factorial av det virkelige datasettet => 1, 2, 3, 4, 5.
- x! = x * (x-1) * (x-2) * (x-3) * …… 3 * 2 * 1
- 5! = 5 * (5-1) * (5-2) * (5-3) * (5-4)
- 5! = 5 * 4 * 3 * 2 * 1
- 5! = 120
Relevans og bruk av Poisson distribusjonsformel
Poisson-distribusjon kan fungere hvis datasettet er en diskret distribusjon, hver forekomst er uavhengig av de andre hendelsene som skjedde, beskriver diskrete hendelser over et intervall, hendelser i hvert intervall kan variere fra null til uendelig og betyr at et antall forekomster må være konstant gjennom hele prosessen. Avhengig av verdien av parameter (λ), kan fordelingen være unimodal eller bimodal. Poisson-distribusjonen er en diskret distribusjon, betyr at hendelsen bare kan oppgis som skjer eller ikke skjer, noe som betyr at tallet bare kan oppgis i hele tall. Brøkforekomster av hendelsen er ikke en del av denne modellen. Utfallsresultatene kan klassifiseres som suksess eller fiasko. Dette er mye brukt i en verden av:
- Dataanalyse for prediktiv analyse av data
- Aksjemarkedspådommer
- Salgsmarkedspådommer
- Forutsigelser om tilbuds- og etterspørselskjeden
- Lett tilgjengelig på Amazon Web Services (AWS) plattformer
- Gjennomgå og vurdere forretningsforsikringsdekning
Andre anvendelser av Poisson-distribusjonen kommer fra mer åpne problemer. For eksempel kan det brukes til å bestemme minimumsbeløpet av ressurser som trengs i et telefonsenter basert på gjennomsnittlige mottatte anrop og samtaler på vent. Kort sagt, listen over applikasjoner kan legges til mer og mer, ettersom den brukes over hele verden praktiske statistiske formål.
Poisson Distribution Formula Calculator
Du kan bruke følgende Poisson distribusjonsberegner
| λ | |
| x | |
| P (x) | |
| P (x) = | (e- λ * λ x ) / x! | |
| (0 -0 * 0 0 ) / 0! = | 0 |
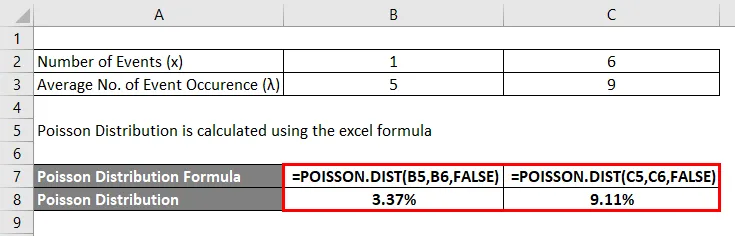
Poisson distribusjonsformel i Excel (med Excel-mal)
Her vil vi gjøre et annet eksempel på Poisson-distribusjonen i Excel. Det er veldig enkelt og enkelt.
Beregn Poisson-distribusjonen i Excel ved å bruke funksjonen POISSON.DIST.
Nedenfor er Syntax of Poisson Distribution formelen i Excel.

Poisson-distribusjonen har følgende argument:
Hvor,
- x = Antall forekomster som sannsynlighet må være kjent for.
- Gjennomsnitt = Gjennomsnittlig antall forekomster i tidsperioden.
- Kumulativ = dens verdi vil være usann hvis vi trenger den eksakte forekomsten av en hendelse og sann hvis et antall tilfeldige hendelser vil være mellom 0 og den hendelsen.

Poisson Distribusjon beregnes ved å bruke excel-formelen
Anbefalte artikler
Dette har vært en guide til Poisson Distribution Formula. Her diskuterer vi Hvordan beregne Poisson Distribusjon sammen med praktiske eksempler. Vi tilbyr også en Poisson Distribusjonskalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Kalkulator for standard normal distribusjonsformel
- Beregning av T-distribusjonsformel med Excel-mal
- Formel for å beregne variansanalyse
- Hva er formue for nettoformue?