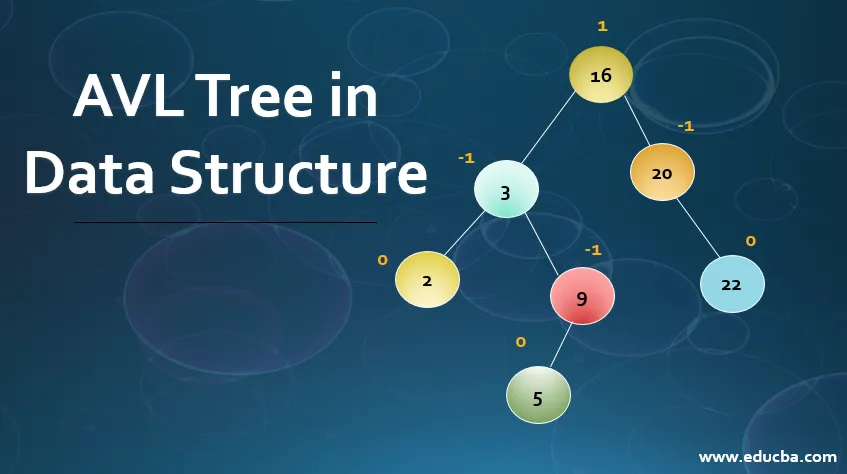
Introduksjon til AVL-tre i datastruktur
AVL-tre i datastruktur refererer til Adelson, Velski & Landis Tree. Dette er en forbedret versjon av det binære søketreet. Det har alle funksjoner som i Binary Search Tree, men avviker bare når de opprettholder en forskjell mellom høyden på det venstre under-treet og det høyre under-treet, og sikrer også at dets verdi er <= 1 i treet, dette kalles balanse faktor.
Balance Factor = height(left-subtree) − height(right-subtree)
For eksempel: Tenk på følgende trær

I eksemplet over er høyden til høyre under-tre = 2 og venstre = 3 og dermed BF = 2 som er <= 1, og dermed sies tre å være balansert.
Hvorfor trenger vi et AVL-tre i DS?
Mens vi jobber med Binary Search Tree, kommer vi over et scenario der elementene er i sortert rekkefølge. I slike tilfeller er alle elementene i arrayet anordnet på den ene siden av roten, dette fører til en økning i tidskompleksiteten til å søke etter et element i en matrise og kompleksiteten blir- O (n) dvs. verste fall kompleksiteten til treet . For å løse slike problemer og redusere søketiden ble AVL-trær oppfunnet av Adelson, Velski & Landis.
Eksempel:

I figuren over var Høyden på venstre undertrinn = 3 som
Høyde på høyre undertråd = 0
Dermed balansefaktor = 3-0 = 3. Dermed har søking etter et element i et slikt tre O (n) av kompleksitet som ligner lineært søk. For å unngå at det kompliserte AVL-treet ble introdusert der hver node i treet trenger å opprettholde
balansefaktor <= 1, ellers skal forskjellige rotasjonsteknikker utføres for å balansere et slikt tre.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Typer rotasjoner
Når balansefaktoren for treet ikke tilfredsstiller <= 1 tilstand, må det utføres rotasjoner på dem for å gjøre det til et balansert tre.
Det er fire typer rotasjoner:
1. Venstre rotasjon: Hvis tilsetningen av en node til høyre for treet gjør det ubalanse, må i så fall Venstre rotasjon utføres.
2. Høyre rotasjon: Hvis tilsetning av en node til venstre for treet gjør noden ubalanse, må høyre rotasjon utføres. Med andre ord, når antall noder øker på venstre side, kommer det frem et behov for å forskyve elementene til høyre side for å balansere det, og det sies å være høyre rotasjon.
3. Venstre-høyre-rotasjon: Denne typen rotasjon er en kombinasjon av de to rotasjonene ovenfor som er forklart. Denne rotasjonstypen oppstår når ett element legges til høyre undertrinn til et venstre tre.
I et slikt tilfelle skal du først utføre venstre rotasjon på undertråden etterfulgt av en høyre rotasjon av venstre tre.
4. Høyre-venstre rotasjon: Denne rotasjonstypen er også sammensatt av en sekvens på over 2 rotasjoner. Denne typen rotasjon er nødvendig når et element legges til venstre for høyre undertrinn og treet blir ubalansert. I et slikt tilfelle utfører vi først høyre rotasjon på høyre undertrinn og deretter venstre rotasjon på høyre tre.
Drift på AVL-tre i DS
Nedenfor tre operasjoner som kan utføres på AVL-treet: -
1. Søk
Denne operasjonen ligner på å utføre et søk i Binary Search Tree. Trinn som følges er som nedenfor:
- Les elementet levert av brukeren si x.
- Sammenlign elementet fra roten, hvis det er det samme, avslutt ellers gå til neste trinn.
- Hvis x
Ellers gå til riktig barn og sammenlign igjen.
Følg prosessene B og C til du finner elementet og avslutter.
Denne prosessen har O (log n) kompleksitet.
Eksempel:
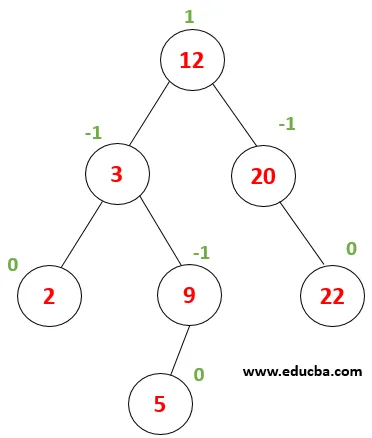 | Tenk på dette treet, der vi må utføre et søk etter nodeverdi 9. La først x = 9, rotverdi (12)> x deretter, verdien må være i venstre undertrinn til rotelementet. |
 | Nå sammenlignes x med nodeverdi 3 x> 3 og dermed må vi fortsette mot riktig undertrinn. |
 | Nå sammenlignes x med node (9), der 9 == 9 returnerer true. Dermed fullføres elementsøking i treet. |
2. Innføring
Når du setter inn et element i AVL-treet, må vi finne det bestemte elementet som må settes inn, og deretter er elementet festet på samme måte som en innsetting i BST, men etter det blir det sjekket om treet fremdeles er balansert eller ikke dvs. balansefaktor for en node er <= 1. Og spesielle rotasjoner utføres etter behov.
Kompleksitet er O (log n).
Eksempel: Tenk på treet nedenfor
 | Hver node har en balansefaktor som 0, -1 eller 1, og dermed er treet balansert. La nå hva som skjer når en node med verdi 1 er satt inn. Det første treet krysses for å finne stedet der det må settes inn … 1 <2 er således skrevet som et venstre barn av noden (2). |
 | Etter innsetting blir noden (9) ubalanse med en balansefaktor = 2. Nå blir den utsatt for å gjennomgå høyre rotasjon. |
 | Et tre blir balanse etter høyre rotasjon, og dermed er innsettingsoperasjonen fullført. |
3. Sletting
Slette et element i AVL-treet inkluderer også å søke etter et element i treet og deretter slette det. Søkeoperasjonen er den samme som BST, og etter å ha funnet elementet som skal slettes fjernes elementet fra treet og elementene blir justert slik at det blir BST igjen. Etter at disse elementene er kontrollert for å ha en balansefaktor på 0, -1 eller 1, og dermed utføres passende rotasjoner for å gjøre det balansert.
Kompleksitet hvis O (log n).
 | Tenk på det gitte treet, som alle har en balansefaktor på 0, -1 eller 1. La oss nå slette en node med verdi 16. Det første treet krysses for å finne noden med verdi 16 som en søkealgoritme. |
 | Node 16 vil bli erstattet med inngangsforgjengeren til denne noden som er det største elementet fra venstre undertre, dvs. 12 Treet har blitt ubalansert og dermed må LL - rotasjon utføres. |
 | Nå har hver node blitt balansert. |
Konklusjon - AVL-tre i datastruktur
AVL-tre er en etterkommer av Binary Search Tree, men overvinner sin ulempe med økende kompleksitet i tilfelle elementene blir sortert. Den overvåker balansefaktoren til treet til å være 0 eller 1 eller -1. I tilfelle det tre blir ubalansert utføres tilsvarende rotasjonsteknikker for å balansere treet.
Anbefalte artikler
Dette er en guide til AVL-tre i datastruktur. Her diskuterer vi Introduksjon, operasjoner på AVL-tre i DS og typer rotasjoner. Du kan også gå gjennom de andre relaterte artiklene våre for å lære mer–
- jQuery Elements
- Hva er datavitenskap
- Typer trær i datastruktur
- C # Datatyper