
Eksempel på standardavviksformel (innholdsfortegnelse)
- Formel
- eksempler
Eksempel på standardavviksformel
I statistikk er standardavviket i utgangspunktet et mål for å finne spredningen av datasettverdiene fra middelverdien til datasettet. Den måler avstanden til datapunktet og middelverdien. Så høyere standardavvik, desto større blir spredningen, og datapunktene har en tendens til å være langt fra gjennomsnittet. Tilsvarende betyr lavere standardavvik at datapunkter vil være nærmere gjennomsnittet. Det er veldig nyttig når du sammenligner datasett som kan ha samme middelverdi, men et annet område.
Beregn vanligvis standardavviket for populasjonsdata, men noen ganger er populasjonsdata så enormt at det ikke er mulig å finne standardavviket for det. I så fall blir standardstandardavvik beregnet, og det vil bli representativt for populasjonsstandardavvik. Så vi vil anta at utvalget er riktig representasjon av befolkningen og vil fokusere på standardstandardavvik i denne artikkelen.
Anta at du har et datasett X med datapunkter (X1, X2 …… ..Xn).
Formelen for populasjonsstandardavvik er gitt av:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
I tilfelle du ikke får hele befolkningen og bare har et utvalg (La oss si at X er prøvedatasettet for populasjonen), blir formelen for standardstandardavvik gitt av:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Hvor:
- X i - i verdien av datasettet
- X m - Gjennomsnittsverdi for datasettet
- n - Totalt antall datapunkter
Formelen kan se forvirrende ut med det første, men det er virkelig å jobbe videre. Følgende er trinnene som kan følges for å beregne prøvestandardavvik:
- Finn antall poeng i datasettet, dvs. n
- Så er neste trinn å finne gjennomsnittsverdien på prøven. Det er i utgangspunktet gjennomsnittet av alle verdiene.
- Etter det, for hvert datapunkt, finner du forskjellen på det fra gjennomsnittet og firkanter det deretter.
- Ta sum alle verdiene i trinnet ovenfor og del det med n-1.
- Det siste trinnet er å ta kvadratroten av antallet beregnet over.
Det er en annen måte å beregne populasjons- og standardavvik ved å bruke STDEV.P () -funksjonen for populasjonsstandardavvik og STDEV.S () -funksjonen for prøvestandardavvik i excel.
Eksempler på standard standardavviksformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av prøven standardavvik på en bedre måte.
Du kan laste ned denne prøven standardavviksformel Excel-mal her - Eksempelstandardavviksformel Excel-malEksempel på standardavviksformel - eksempel # 1
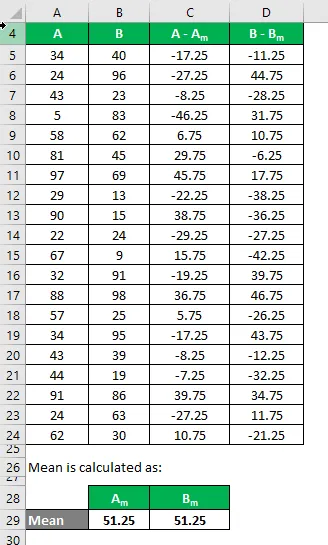
La oss si at vi har to utvalgte datasett A & B, og hver inneholder 20 tilfeldige datapunkter og har samme gjennomsnitt. Beregn prøven standardavvik for datasettet A & B.
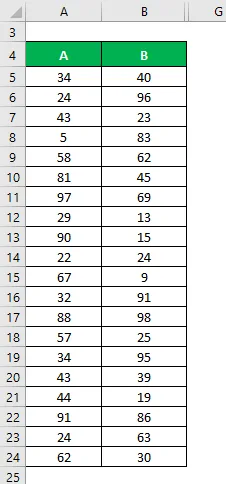
Løsning:
Gjennomsnitt beregnes som:
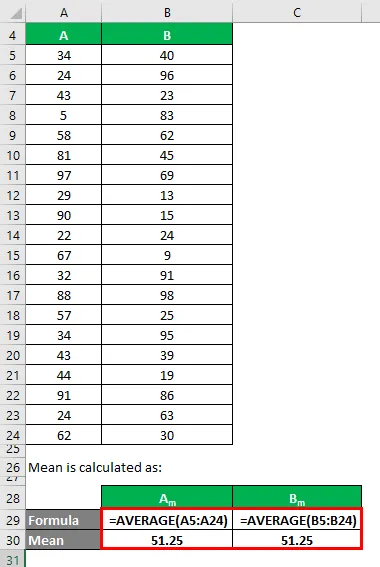
- Gjennomsnitt av datasett A = 51, 25
- Gjennomsnitt av datasett B = 51, 25
Nå må vi beregne forskjellen mellom datapunktene og middelverdien.
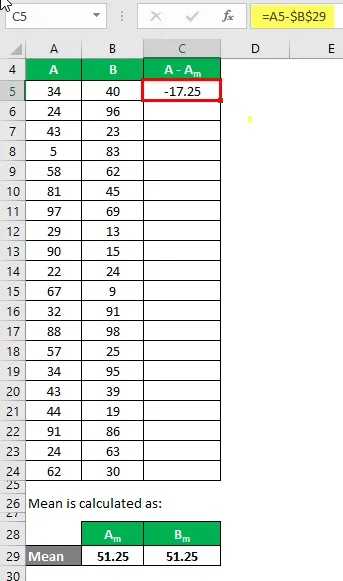
På samme måte beregner du for alle datasettet til A.
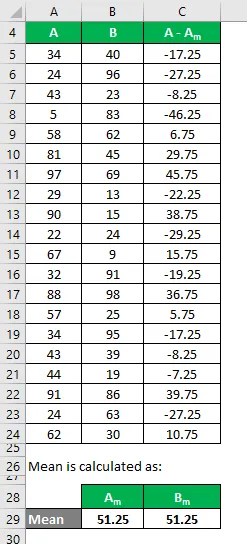
På samme måte kan du også beregne det for datasett B.
Beregn kvadratet av forskjellen for både datasettene A og B.
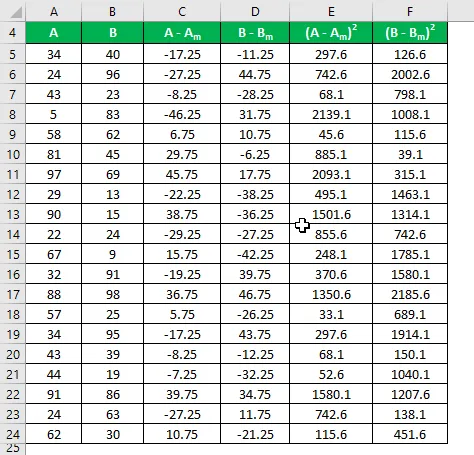
Eksempel på standardavvik beregnes ved å bruke formelen nedenfor
Eksempel på standardavvik = √ (Σ (X i - X m ) 2 / (n - 1))
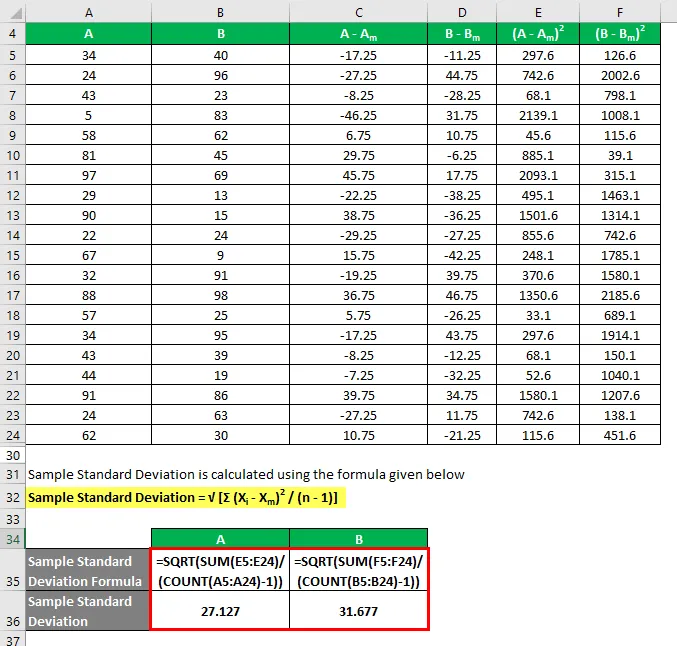
Så hvis du ser her, selv om begge datasettene har samme middelverdi, har B et mer standardavvik som A, noe som betyr at datapunktene til B er mer spredt enn A.
Eksempel på standardavviksformel - eksempel # 2
La oss si at du er en veldig risikovillig investor, og at du ønsker å investere penger i aksjemarkedet. Siden risikovilligheten din er lav, vil du investere i trygge aksjer som har lavere standardavvik. Din økonomiske rådgiver har foreslått deg 4 aksjer du kan velge mellom. Du vil velge to aksjer blant disse 4, og du vil bestemme det på grunnlag av lavere standardavvik.
Du har fått informasjon om historisk avkastning de siste 15 årene.
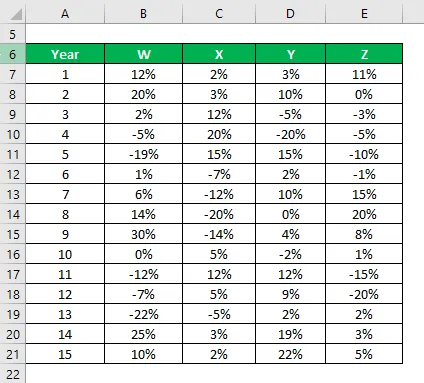
Løsning:
Eksempelstandardavvik beregnes ved å bruke excel-formelen
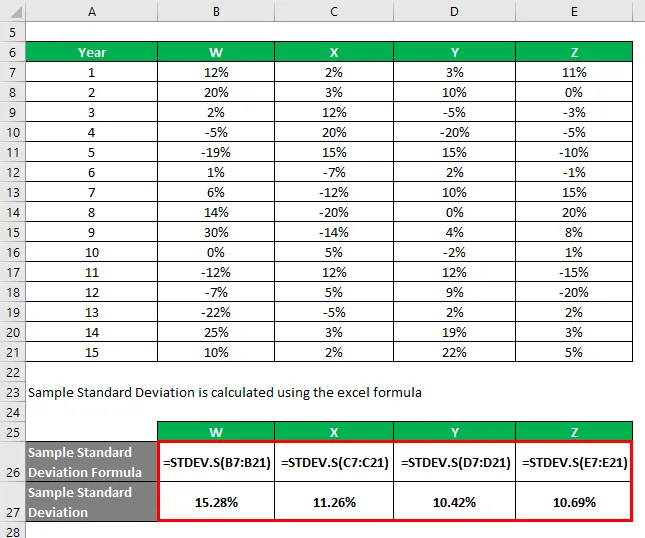
Basert på informasjonen og prøven standardavvik, vil du velge aksje Y og Z å investere siden de har det laveste standardavviket.
Forklaring
Vi diskuterer betydningen av standardavvik fra et statistisk synspunkt, men det spiller også en viktig rolle hvis vi snakker om et økonomisk synspunkt. I finans er det i utgangspunktet målet på risiko en investering bærer og hvor risikabel den investeringen er. Basert på risikoen en investering har, kan investorer deretter beregne minimumsavkastningen de trenger for å kompensere den risikoen. Som i eksemplet ovenfor, siden Y og Z har et mindre standardavvik, betyr det at det er mindre variasjon i avkastningen på disse aksjene, så de er mindre risikofylte. Ett poeng mens vi bruker standardavviksverktøy, må vi huske at det er sterkt påvirket av ekstreme verdier eller utliggere. Disse outliers kan skjev standardavviksverdien.
Relevans og bruksområder for standard standardavviksformel
Standardavvik hjelper investorene og analytikeren med å finne risiko- og belønningsgraden eller Sharpe-forholdet for en investering. I utgangspunktet kan hvem som helst tjene en risikofri avkastning ved å investere i statskasser og risikofri verdipapirer. Men avkastning utover dette er meravkastningen, og for å oppnå det, er risikonivået du må ta et mål på Sharpe-forholdet:
Sharpe Ratio = (avkastning på investering - risikofri rente) / standardavvik
For å øke Sharpe-forholdet, er investeringen bedre.
Som vi sa at standardavvik er et mål på risiko, men lavere standardavviksverdi er ikke alltid å foretrekke. Hvis en investor har en høyere risikoappetitt og ønsker å investere mer aggressivt, vil han være villig til å ta mer risiko og foretrekker et relativt høyere standardavvik enn en risikovillig investor. Så det kommer an på hvilket risikonivå en investor er villig til å ta.
Anbefalte artikler
Dette har vært en guide til eksempler på standardavviksformel. Her diskuterer vi hvordan du beregner prøven standardavvik sammen med praktiske eksempler og nedlastbar excel-mal. Du kan også se på følgende artikler for å lære mer -
- Eksempler på populasjonsvariasjonsformler
- Kalkulator for relativ standardavvik
- Hvordan beregne standard normal distribusjon?
- Beregning av binomial distribusjon