Komplekse tall i MATLAB - Hvordan generere komplekst antall?

Introduksjon til komplekse tall i MATLAB

Komplekse tall er kombinasjonen av reelle tall og imaginære tall i form av p + qi der p og q er de reelle tallene og i er det imaginære tallet. Et tenkt tall er definert der i er resultatet av en ligning a 2 = -1. Vi kan bruke i eller j til å betegne de imaginære enhetene. Som komplekse tall brukes i alle matematiske beregninger, og Matlab brukes hovedsakelig til å utføre matematiske beregninger. Så komplekse tall utgjør en viktig del av å lære Matlab.

Kompleks antall generasjon i MATLAB

Komplekse nummer kan opprettes eller deklareres i Matlab ved å bruke en 'kompleks' funksjon. Vi kan også lage komplekse tall ved å finne kvadratroten til et hvilket som helst negativt tall. I Matlab kan vi bruke i eller j til å betegne den imaginære delen av det komplekse tallet.

eksempler

X = 4 + 5i

Her er X et sammensatt antall som inneholder 2 deler, dvs. ekte og tenkt del. 4 er den virkelige delen og 5 er den imaginære delen. Vi kan finne de virkelige og imaginære delene ved å bruke funksjoner i Matlab.

a = ekte (X) = 4 (Dette gir den reelle delen av det komplekse tallet)
b = imag (X) = 5 (Dette gir den imaginære delen av det komplekse tallet)
kompleks (6, 7) = 6 + 7i (Denne funksjonen brukes til å lage komplekse tall)

Vi kan også lage komplekse matriser i Matlab som også kan deklareres ved bruk av de komplekse funksjonene.

a = kompleks (x, y)

Det er visse forhold for x og y som vi skal følge som x og y ikke skal være enkelt eller dobbelt. Et komplekst skalar kan opprettes hvis to innganger er skalare i naturen,

X = kompleks (5, 3)
X = 5, 0000 + 3, 0000i

Tilsvarende kan det opprettes en kompleks vektor hvis vi har to innganger som vektorer.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = kompleks (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Vi kan lage et komplekst tall som bare har en skalar som,

X = kompleks (10)
X = 10.0000 + 0.0000i

Det er visse forhold som input- og output-argumentene skal følge,

Inngangsargumentene inneholder virkelige og imaginære deler som x hvilken som helst y. x og y skal være skalar, vektor, flerdimensjonal matrise eller matrise i MATLAB. x- og y-størrelsen skal være den samme. De skal være av samme datatype, men det er få unntak som dobbelt kan brukes med enkelt og heltall kan kombineres med en dobbel som er skalær.

Utgangen fra matrisen kan være vektor, skalar, matrise eller flerdimensjonal matrise avhengig av inngangsargumentene. Størrelsen på utgangen skal være den samme som inngangen. Hvis inngangsargumentene er av forskjellige datatyper enn output bestemmes av,

Hvis et av inngangsargumentene har en enkelt art, bør utdataene også være enkelt.
Hvis en av inngangsargumentene har et helt tall, skal utdataene være av en hel datatype.

Vi kan sjekke om matrisen er ekte eller imaginær ved å bruke isreal funksjon.

Kode:

X = (2+i, 1); Isreal(X)

Produksjon:

Kode:

Isreal (X (2))

Produksjon:

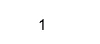
For å trekke ut de virkelige og imaginære delene, kan vi bruke virkelige og imagefunksjoner i Matlab som,

Kode:

real(X)

Produksjon:

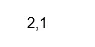
Kode:

imag(X)

Produksjon:

Drift og funksjoner av komplekse tall i MATLAB

Det er flere operasjoner og funksjoner som kan utføres ved bruk av komplekse tall i Matlab som

abs: Denne funksjonen brukes til å finne modulen til et hvilket som helst komplekst tall i form av p + qi. abs (2 + 3i) = kvadratrot av (2 2 + 3 2) = (13) 0, 5
vinkel: For å finne fasevinkelen til det komplekse tallet.

Det er visse tips som bør følges for at komplekse tall i Matlab fungerer som de skal,

Vi bør unngå å bruke i og j som en del av alle variabelnavn, ettersom de brukes til å betegne de imaginære delene av det komplekse tallet.
Vi bør unngå å bruke j eller i hvis den imaginære delen er 1. I stedet kan vi bruke 1j eller 1i.
Vi kan lage en kompleks funksjon i Matlab når i og j brukes som variabelnavn i noen del, inngangsargumentene er ikke av en eller to typer og den imaginære delen er null.

Konklusjon

Komplekse tall brukes i det matematiske eller ingeniørfaglige området. Mange virkelige eller praktiske anvendelser kan beskrives ved å bruke den imaginære delen av komplekse tall. Så å forstå bruken og bruken av komplekse tall på forskjellige plattformer er viktig, spesielt hvis du har å gjøre med et fysisk eller matematisk domene.

Anbefalte artikler

Dette er en guide til komplekse tall i MATLAB. Her diskuterer vi introduksjon og kompleks tallgenerering i matlab inkludert eksempler med drift og funksjon. Du kan også se på følgende artikler for å lære mer-