Vektorer i Matlab - Typer av vektordrift med eksempler

Introduksjon til vektorer i Matlab

En vektor er et lukket sett med elementer. I Matlab kan vi lage vektorer ved å bruke firkantede parenteser. Vektorer er en av illustrasjonene av matriser (endimensjonal matrise). det kan være representert på to måter radvektor og kolonnevektor.

Radvektor

Det er horisontalt sett med elementer. Det er representert i firkantede parenteser. Hvert element skilles med komma eller mellomrom.

X = (4 7 8) eller X = (4, 7, 8)

Kolonnevektor

Det er et vertikalt sett med elementer. Det er også representert i firkantede parenteser. Det er to måter å lage kolonnevektorer først ved å skille hvert element med et semikolon og en annen måte er å skrive hvert element på neste rad i kommandovinduet.

X = (4; 6; 7) eller

X = (4

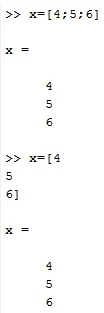
Vektoroperasjoner

Vektoroperatører er stort sett klassifisert i to kategorier.

1. Aritmetisk drift

La oss vurdere to vektorer x og y med verdiene x = (1 4 5 3) og y = (5 3 2 1) vi kan utføre forskjellige operasjoner på disse to vektorene x og y.

en. Multiplikasjon: Denne funksjonen brukes til å multiplisere med hvilken som helst aritmetisk verdi til hele vektoren.

For eksempel:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Syntaks: variable name = arithmetic constant * vector name

b. Trigonometrisk funksjon: Vi kan bruke enhver trigonometrisk funksjon på vektorlignende synd, kos, solbrun, kosek, sek osv.

Eksempel tri = cos (x)

Svaret er: 0.54 - 0.65 0.28 -0.99

Syntaks: variable name = trigonometric function name ( vector name )

Sum: Dette viser totalt (tillegg av) hele elementer i en vektor.

Eksempel

x = (1 4 5 3)

Totalt = sum (x)

Produksjonen er totalt = 13

Syntaks: variable name = = sum ( vector name )

c. Lengde: Den viser lengden på en bestemt vektor, la oss en vektor p = (9 7 5 3 1 9 7 5 3 1)

Eksempel

p = (9 7 5 3 1 9 7 5 3 1)

Len = lengde (p)

Utgang er Len = 10

d. Tilsetning av vektorer: Tilsetning av to eller flere vektorer er enkel betjening i Matlab, la oss vurdere to vektorer p og q.

P = (4 6 3 2) og q = (5 7 9 1)

Legg til = p + q

Output er Add = (9 13 12 3)

Syntaks: vector name operator ( + ) vector name

På samme måte kan vi gjøre subtraksjon som sub = p - q

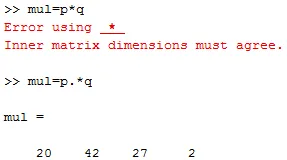
e. Multiplikasjon av vektorer: Hvis vi vil gjøre multiplikasjon av to vektorer, vil en enkel multiplikasjonsoperatør (*) ikke fungere. Derfor må vi legge til en prikkoperator ('.') Med en multiplikasjonsoperatør.

Eksempel:

P = (4 6 3 2) og q = (5 7 9 1)

mul = p. * q

utgang er mul = (20 42 27 2)

Syntaks: variable name = vector name dot operator multiplication operator vector name

Anta at jeg vil finne ut kvadratet av en bestemt vektor, eller at jeg bare vil multiplisere vektor med den vektoren.

Da vil syntaks være squr = x. 2

2. Relasjonell drift

en. Tilsvarende som operatøren : denne operatøren sammenligner hvert n hvert element fra to vektorer og gir utdata er null og en form.

Eksempel

m = (2 5 8)

Og n = (5 5 3)

Som vi vet er det tre elementer i vektor m og vektor n,

m == n

Ovennevnte utsagn vil gi utdata som 0 1 0, noe som betyr at første nei ikke er likt, det andre tallet er lik og det tredje nei er ikke likt. O representerer usant og 1 representerer sant.

b. Mindre enn operatøren (<): Mindre enn operatøren representerer med symbolet '<'. vi kan sammenligne en gitt matrise med hvilken som helst aritmetisk konstant eller med en hvilken som helst annen vektor.

Eksempel

m = (3 2 4)

n = (1 1 1)

m <n

utgangen vil være 0 0 0, det betyr at alle tall er større enn vektor n.

og hvis m <10

da blir utgangen 1 1 1, det betyr at alle tall er mindre enn 10.

c. Større enn operatør (>): Større enn operatøren representerer med symbolet ('>'). Vi kan sammenligne en gitt matrise med hvilken som helst aritmetisk konstant eller med en hvilken som helst annen vektor.

Eksempel:

M = (3 2 4)

N = (1 1 1)

m> n

Utgangen vil være 1 1 1, det betyr at alle verdiene er større enn verdiene til vektor n.

Konklusjon - Vektorer i Matlab

I Matlab kan vi lage forskjellige typer vektorer der vi kan utføre forskjellige operasjoner som addisjon, subtraksjon, multiplikasjon, kvadrat, kvadratrot, kraft, skalering, vektormultiplikasjon, prikkprodukt, etc.

Anbefalte artikler

Dette er en guide til vektorer i Matlab. Her diskuterer vi hvilke typer vektordrift som inkluderer aritmetisk og relasjonell drift sammen med noen eksempler. Du kan også se på følgende artikler for å lære mer -