
Introduksjon til Fibonacci-serien i Python
Fibonacci-serien i Python, blir dette referert til som en serie med tall, der det neste tallet er summen av de nåværende to tallene.
For eksempel:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. så videre
Så her 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 og så videre.
Ser vi på det ovennevnte, ville man ha fått en viss ide om hva vi snakker om.
Når det gjelder matematisk regel, kan det imidlertid skrives som:

Hvor det niende tallet er summen av tallet på steder (n-1) og (n-2). Når det gjelder implementering av Fibonacci-serien, kan det være et antall kodespråk som det kan gjøres gjennom.
Imidlertid er Python et mye brukt språk i dag. La oss se implementeringen av Fibonacci-serien gjennom Python. Man bør være klar over grunnleggende kondisjoneringsuttalelser som loop, hvis-ellers, mens loop osv. I Python, før du fortsetter her. Hvis ikke, vil det være flott om man kan revidere det og deretter ta opp det kommende innholdet. Her for demonstrasjonsformål bruker jeg spyder som er IDE for programmeringsspråk for python. Man kan bruke hvilke som helst andre IDE- eller Ipython-notatbøker også for utførelse av Python-programmene.
Fibonacci-serien i Python
La oss se implementeringen av Fibonacci-nummer og serier med tanke på første to elementer i Fibonacci er 0 og 1:
Imidlertid kan du finjustere funksjonen til Fibonacci etter ditt krav, men se det grunnleggende først og gradvis gå videre til andre.
Python-kode for å finne Nth Fibonacci-nummer
Kode 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Kode 2:
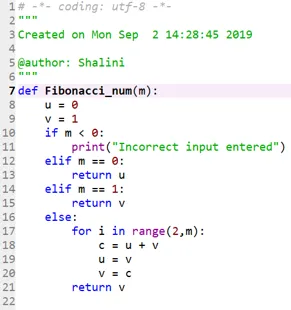
Produksjon:
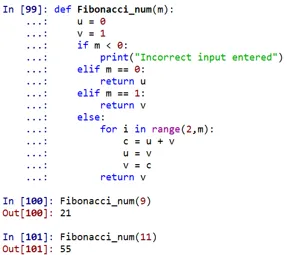
Som man kan se, ville Fibonacci-tallet på 9. plass være 21, og på 11. plassering ville være 55.
- Her er "Chart_num" en definert funksjon, som tar seg av å finne Fibonacci-nummeret ved hjelp av visse betingelser. Denne funksjonen kan kalles ved å spesifisere hvilken som helst posisjon.
La oss se hvordan man kan skrive ut serier til den nevnte stillingen:
Kode:
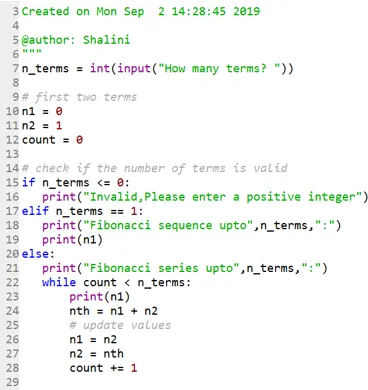
Produksjon:
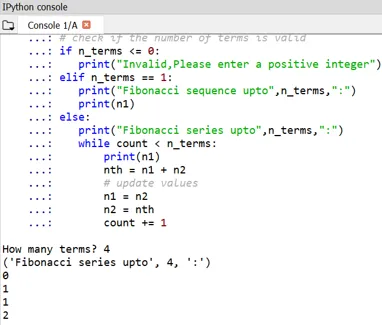
Man kan merke at starten på Fibonacci-tall er definert som 0 og 1.
- Hvis noen ønsker å definere sine egne begrep, kan det også gjøres på samme måte ved å finpusse n1 og n2. Her er eksemplet for det:
La oss si at vi nå ønsker at startbetingelsene våre er: n1 = 3, n2 = 5
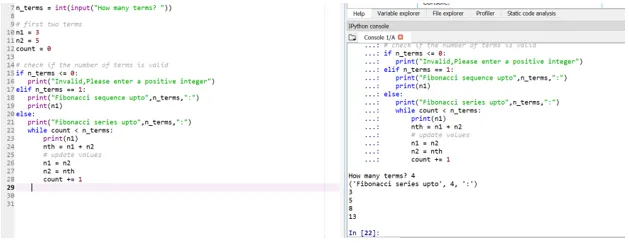
Så her vil din fjerde terminposisjon (brukerinnspill tas) avgjøres basert på startbetingelsene.
Metoder som Fibonacci-serien kan genereres gjennom
Nedenfor er de tre metodene, gjennom hvilke Fibonacci-serier kan genereres:
1. Gjennom generatorer
Kode:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Produksjon:
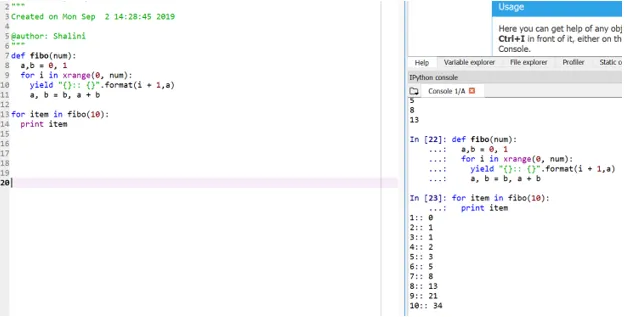
Denne metoden blir referert til som "generator" fordi funksjonen xrange er en generator med tallene mellom 0 og num og utbytte er generatoren for formatert utgang.
Dette er hva xrange gjør for deg:

Her er Fibonacci-serien blitt definert i form av funksjon, inne i hvilken for loop, xrange og yield-funksjonen tar seg av output.
2. Gjennom for loop
Kode:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Produksjon:

Som man kan se, har enkle for loop blitt brukt, for å skrive ut Fibonacci-serien mellom 0 til 10. Innvendig for sløyfe har nye verdier blitt tildelt variablene. U og v er standardverdiene for Fibonacci som er satt til henholdsvis 0 og 1.
Når det gjelder loop løper, er den nye u-verdien den gamle v-verdien, mens den nye v-verdien er summen av gamle verdier for u og v. Dette fortsetter til slutten av rekkeverdiene.
3. Gjennom rekursjon
Kode:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Produksjon:
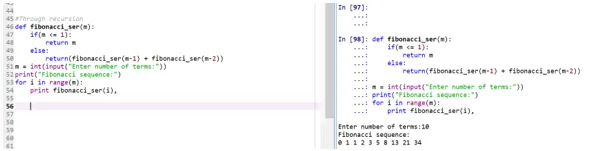
- Funksjonen "retracement_ser" ringer til seg selv å skrive ut Fibonacci-serien.
- Og derav har metoden fått navnet "rekursjon".
Trinn fulgt her:
- Her har brukeren blitt bedt om å legge inn stedet til hvilken Fibonacci-serien må skrives ut.
- Nummer passerer gjennom funksjonen "retracement_ser".
- Tilstanden blir sjekket, hvis den oppgitte lengden er mindre enn 1 eller ikke. Hvis ja, blir resultatet gitt umiddelbart.
- Men hvis lengden er større enn 1, blir rekursive samtaler foretatt til "retracement_ser" med argumenter med lengde mindre enn 1 og 2, dvs. retracement_ser (m-1) og retracement_ser (m-2).
- Derfor gir rekursjon ønsket utskrift og skriver den ut.
- Så kort sagt diskuterte vi tre måter å vise Fibonacci-serien på.
- Gjennom for loop, gjennom generatorer og gjennom rekursjon.
Alle tre Python-kodene er oppsummert
Nedenfor er de tre pytonkoden:
1. Gjennom generatorer
Kode:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Gjennom for loop
Kode:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Gjennom rekursjon
Kode:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Oppsummert ovenfor er alle prosedyrer, man må øve for å få et godt grep om alle.
Produksjon:
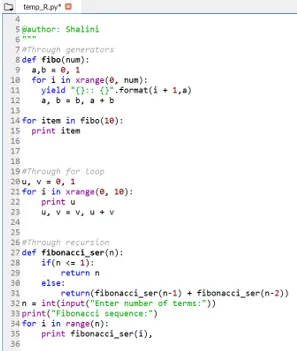
Konklusjon
Ved å gå gjennom innholdet ovenfor i Fibonacci, ville man ha fått krystallklar forståelse av Fibonacci-tall og -serier, spesialisert med python. En gang blir man komfortabel med logikken i Fibonacci-serien, og genererer et nytt sett med serier, jobber med andre tall og med forskjellige metoder vil nå være en kakevalk for deg. En logisk tilnærming er den eneste måten å utmerke seg i dette.
Anbefalte artikler
Dette er en guide til Fibonacci-serien i Python. Her diskuterer vi Fibonacci-tall og -serier, spesialisert med python, genererer et annet sett med serier, jobber med andre tall og med forskjellige metoder. Du kan også gå gjennom andre relaterte artikler for å lære mer -
- Tilfeldig nummergenerator i Python
- Matematiske funksjoner i Python
- Factorial i Python
- Innkapsling i Python
- Fibonacci-serien i Java
- Python-funksjoner
- Factorial-program i JavaScript
- Tilfeldig nummergenerator i Matlab
- Tilfeldig nummergenerator i C #
- Innkapsling i JavaScript