CAPM-formelen (innholdsfortegnelse)
- CAPM-formelen
- CAPM-kalkulator
- CAPM-formel i Excel (med Excel-mal)
CAPM-formelen
Det lineære forholdet mellom forventet avkastning og den systematiske risikoen er representert av CAPM-formelen (Capital Asset Pricing Model).
CAPM beregnes i henhold til formelen nedenfor: -
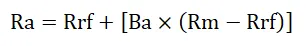
Hvor:
- Ra = Forventet avkastning på en investering
- Rrf = Risikofri rente
- Ba = Beta for investeringen
- Rm = Forventet avkastning på markedet
Og risikopremie er forskjellen mellom forventet avkastning på markedet minus risikofri rente (Rm - Rrf) .
Markedsrisikopremie
Markedsrisikopremien er meravkastningen, dvs. belønningen som forventes å kompensere en investor for å ta opp risikoen som ligger i porteføljen da investeringer i aksjemarked alltid er høyere enn å investere i statsobligasjoner. Derfor er det en forskjell mellom forventet avkastning på markedet og risikofri rente. Markedsrenten, Rm, kan estimeres basert på tidligere avkastning eller anslått fremtidig avkastning. For eksempel brukes de amerikanske statskassene og obligasjonene for risikofri rente.
Forventet tilbakekomst
"Ra" refererer til forventet avkastning på en investering over en periode.
Risikofri rente
"Rrf" angir risikofri rente, som tilsvarer avkastningen på en 10-årig amerikansk statsskatt eller statsobligasjon. Risikofri rente er avkastningen som en investering som ikke tjener noen risiko, men i den virkelige verden inkluderer den risikoen for inflasjon. Risikofri rente skal også være i det landet hvor investeringen gjøres, og obligasjonens løpetid skal også samsvare med investeringsperioden. Normalt er risikofri avkastning som brukes til å estimere risikopremien vanligvis gjennomsnittet av historisk risikofri avkastning og ikke generelt gjeldende risikofri avkastning.
Beta
Betaen som er representert som “Ba” i formlene til CAPM er et mål på volatiliteten til en verdipapir eller en portefølje og beregnes ved å måle hvor mye aksjekursen endres med avkastningen i det samlede markedet. Beta er et mål på systematisk risiko. For eksempel, hvis et selskaps beta er lik 1, 7, betyr det at det har 170% av volatiliteten i avkastningen av markedsgjennomsnittet og aksjekursbevegelsene vil være ganske ekstreme. Hvis betaen er lik 1, er den forventede avkastningen på investeringen lik avkastningen til markedsgjennomsnittet. Hvis betaen er -1, betyr det at aksjekursene er mindre risikable og ustabile.
Bruk av CAPM-modell
Vi vil se noen få eksempler på CAPM som oftest brukes til å bestemme hva den virkelige prisen på en investering skal være. Når vi beregner den risikofylte eiendelens avkastning ved å bruke CAPM, kan den satsen også brukes til å diskontere investeringens fremtidige kontantstrømmer til nåverdien og til slutt komme til investeringens virkelige pris.
Eksempler på CAPM-formel
La oss ta et eksempel for å finne ut CAPM for et selskap: -
Du kan laste ned denne CAPM-formelen Excel-malen her - CAPM-formelen Excel-malenEksempel 1
Si at A forventes å gi avkastning på 14% i løpet av det neste året, og at den nåværende risikofri rente er 6%, og du vil beregne om det er lønnsomt å investere i dette. Du har beregnet aksjens betaverdi som er 1, 7. Det samlede aksjemarkedet har en beta på 1, 0. Dette innebærer at aksjen har et høyere risikonivå enn den totale risikoen. Derfor forventer vi en høyere avkastning enn markedets forventede avkastning på 14% det neste året.
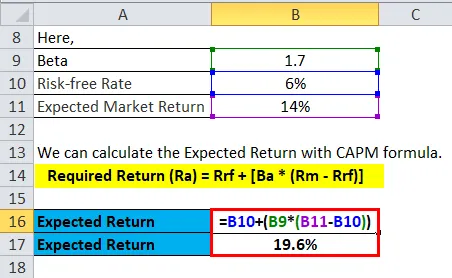
Forventet avkastning kan beregnes som nedenfor:
- Nødvendig retur (Ra) = Rrf + (Ba * (Rm - Rrf))
- Nødvendig avkastning (Ra) = 6% + 1, 7 * (14% - 6%)
- Nødvendig avkastning (Ra) = 6% + 13, 6%
- Nødvendig avkastning (Ra) = 19, 6%
Denne beregningen forteller deg at du vil få 19, 6% på investment.ca
Eksempel 2
La oss anta at en investor tenker å investere i en av de tre aksjene som er tilgjengelige i markedet. Nedenstående informasjon er tilgjengelig for å estimere avkastningstakten for de tre aksjene.
- Aksj A med en beta på 0, 80
- Lager B med en beta på 1, 20
- Lager C med en beta på 1, 50
Risikofri rente er 5, 00% og forventet markedsavkastning er 12, 00%.
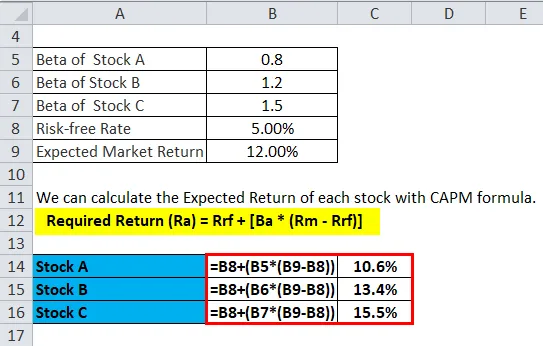
Vi kan beregne forventet avkastning for hver aksje med CAPM-formel.
- Nødvendig retur (Ra) = Rrf + (Ba * (Rm - Rrf))
Forventet retur av lager A
- E (RA) = 5, 0% + 0, 80 * (12, 00% - 5, 0%)
- E (RA) = 5, 0% + 5, 6%
- E (RA) = 10, 6%
Forventet retur av aksje B
- E (RB) = 5, 0% + 1, 20 * (12, 00% - 5, 0%)
- E (RB) = 5, 0% + 8, 4%
- E (RB) = 13, 4%
Forventet retur av aksje C
- E (RC) = 5, 0% + 1, 50 * (12, 00% - 5, 0%)
- E (RC) = 5, 0% + 10, 5%
- E (RC) = 15, 5%
Derfor ser vi at det er best å investere i aksje C. Så man ser at høyere beta, desto høyere blir forventet avkastning i henhold til CAPM-formelen.
Eksempel 3
Nå vil vi se et applikasjonsproblem med forventet avkastning. Vi kan beregne netto nåverdi ved å bruke forventet avkastning eller hekkraten fra CAPM-formelen som en diskontert rente for å estimere nåverdien av en investering
Følgende informasjon er gitt:
- β = 1, 3
- Rrf = 6%
- Rm = 13%
Så hekkfrekvensen eller forventet avkastning fra prosjektet beregnes som nedenfor:
- Nødvendig retur (Ra) = Rrf + (Ba * (Rm - Rrf))
- Ra = 6% + 1, 3 * (13% - 6%)
- Ra = 6% + 9, 1%
- Ra = 15, 1%
Informasjon spesifikt for prosjektet du planlegger å investere er som følger. Tallene er i lakhs:
- Opprinnelig investering = 5 000 dollar
- Forventede utbetalinger: 6 000 dollar på 2. året, 5 000 på femte året
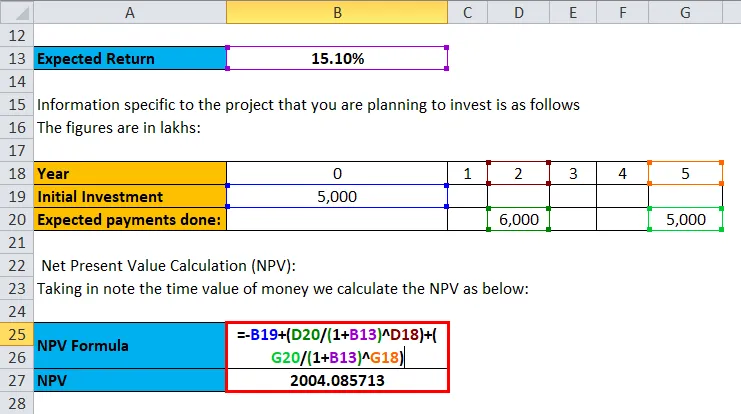
Netto nåverdiberegning (NPV): Tar notatet inn tidsverdien på penger beregner vi NPV som nedenfor:
Npv = - startinvestering + summering av (investeringens verdi / (1+ rente) antall år)
Så innledende investering er 5000, og deretter er 6000 investert i andre år og 5000 på femte år. bare sette verdiene for å få resultatene
- NPV = -5000 + (6000 / 1.151 2) + (5000 / 1.151 5)
- NPV = £ 2004.085713
Derfor er nettoverdien av den investerte investeringen 2004.085713.
Antagelser av CAPM-formelen
- Investorer har diversifisering på tvers av en rekke investeringer slik at de eliminerer usystematisk risiko.
- Investorer kan låne og låne beløp under risikofri rente.
- CAPM anser et marked for å være ideelt og inkluderer ikke beskatning eller transaksjonskostnader på en konto.
- Anta at all informasjon er tilgjengelig samtidig for alle investorer.
- Hver investor er i mot eksponering for risiko.
begrensninger
Begrensningen av denne CAPM-formelen er jo høyere risikoen for eiendelen er, desto større er forventet avkastning som alltid ikke er sant.
CAPM-formelkalkulator
Du kan bruke følgende CAPM-kalkulator
| Rrf (%) | |
| Ba | |
| Rm (%) | |
| Ra | |
| Ra = Rrf + (Ba X (Rm - Rrf)) |
| 0 + (0 X (0 - 0)) = 0 |
CAPM-formel i Excel (med Excel-mal)
Her vil vi gjøre det samme eksemplet med CAPM-formelen i Excel. Det er veldig enkelt og enkelt. Du må oppgi de tre innspillene, dvs. risikofri rente, investeringens beta og forventet avkastning på markedet
Du kan enkelt beregne CAPM ved å bruke formel i malen som følger med.
Forventet avkastning kan beregnes som nedenfor:
Vi kan beregne forventet avkastning for hver aksje med CAPM-formel.
Forventet avkastning fra prosjektet beregnes som nedenfor:

Nettoverdien av investeringen beregnes som:
Anbefalte artikler
Dette har vært en guide til en CAPM-formel. Her diskuterer vi bruksområdene sammen med praktiske eksempler. Vi gir deg også CAPM-kalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Formel for gjeldsgrad
- Veiledning for formel for skattekvivalent avkastning
- Eksempler på formel for pris til inntjening
- Avkastning på gjennomsnittlig formuesformue