
Introduksjon til matematiske funksjoner i C
Denne artikkelen viser de forskjellige matematiske funksjonene som brukes i C-programmeringsspråk med illustrasjon av arbeidskode. Datamaskiner gjør enorme matematiske beregninger og analyser av enorme tall, for å gjøre det har vi brukt matematikkfunksjoner i C. Før vi starter med, må vi vite at C-språk bruker overskrift / bibliotek kalt Math.h for forskjellige matematiske funksjoner. Dette hjelper med å beregne trigonometriske operasjoner, logaritmer, absolutte verdier, kvadratrøtter. Så la oss utforske de forskjellige typer funksjoner som brukes i dette biblioteket. Alle disse funksjonene er doble som datatype og returnerer de samme.
Ulike matematikkfunksjoner i C.
La oss se forskjellige funksjoner definert i matte.h og Math-biblioteket er kategorisert i tre hovedtyper: Trigonometriske funksjoner, matematikkfunksjoner, Log / expo-funksjoner. For å implementere funksjonene nedenfor er det obligatorisk å ta med eller i koden.
1. etasje (dobbel a)
Denne funksjonen returnerer den største heltallverdien som ikke er større enn 'a'. Det runder en verdi og returnerer en dobbel som et resultat. Det oppfører seg annerledes for negative tall, da de avrunder til neste negative tall.
Eks: etasje (7, 2) er 7, 0
etasje (-7, 2) er -8, 0
Eksempel:
Dette programmet illustrerer hvordan du beregner gulvet for den deklarerte verdien og runder til neste verdi 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Produksjon:

2. tak ()
syntaks:
double ceil (double b)
Denne funksjonen returnerer den minste heltallverdien som er større eller lik b og runder verdien oppover. For en negativ verdi beveger den seg mot venstre. Eksempel 3.4 returnerer -3 har utgangen.
Eksempel:
Dette programmet forklarer ved å komme med innspill i float-argumentet og returnerer takverdien.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Produksjon:

3. kvadrat ()
Denne funksjonen returnerer kvadratroten til et spesifisert nummer.
syntaks:
sqrt( arg)
Eksempel:
Koden nedenfor forklarer den mest kjente matematiske funksjonen sqrt () ved å ta 'n' verdier for å beregne kvadratroten for de forskjellige 'n' verdiene.
#include
#include
int main()
(
double n, output;
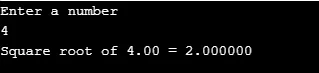
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Produksjon:
4. runde ()
Denne funksjonen avrunder den nærmeste verdien av en gitt inngang. Den kaster feilen hvis verdien er for stor. Andre funksjoner som lround (), llround () runder også det nærmeste heltallet.
syntaks:
int round(arg)
Eksempel:
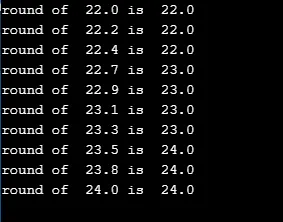
Koden nedenfor er veldig enkel, noe som avrunder til nærmeste r-verdi i for-loopen.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Produksjon:
5. kraft ()
Denne funksjonen går tilbake til strøm for det gitte tallet (a b ). Den returnerer en hevet til kraften til b, som har to parametre base og eksponent.
Eksempel:
I kildekoden nedenfor under lar vi en bruker legge inn en inngangsverdi for å beregne kraften til de gitte to argumentene.
#include
#include
int main()
(
int r, ba, expr;
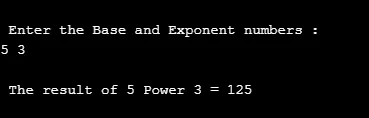
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
produksjon:
6. trun ()
Denne funksjonen hjelper deg med å avkorte den gitte verdien. Det returnerer heltallverdier. For å avkorte flytende og doble verdier trunkef (), brukes trunkl ().
syntaks:
double trunc(a);
Eksempel:
Under kildekoden tar to inndataverdier a, b for å avkutte de doble verdiene.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Produksjon:

7. fmod ()
Denne funksjonen returnerer resten for de gitte to inngangsverdiene når m er delt med n.
syntaks:
double fmod(double I, double j)
Eksempel:
I eksemplet nedenfor tar det to verdier fra brukeren å beregne resten ved hjelp av fmod () -funksjonen.
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Produksjon:

Trigonometriske funksjoner
Nedenfor er de forskjellige funksjonene til Trigonometric:
1. synd ()
Denne innebygde funksjonen gir sinusverdi for det gitte antallet, beregner flytende punktverdier. asin () beregner bue, for hyperbolsk er det sinh ().
syntaks:
return type sin(y);
y returnerer verdi i radianer og returtypen tar dobbelt.
Eksempel:
I den følgende kildekoden har jeg tatt to forskjellige inndataverdier for å beregne sinens verdi og returnerer dobbelt.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
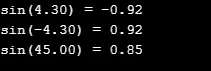
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Produksjon:
2. sinh ()
Denne mattefunksjonen beregner trigonometrisk tangens sinusverdi for det gitte tallet.
syntaks:
double sinh(x);
Eksempel
I kildekoden nedenfor blir Sine hyperbol beregnet ved å deklarere en inngangsverdi.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Produksjon

3. cos ()
Denne mattefunksjonen bestemmer den trigonometriske kosinusverdien for det gitte elementet.
Syntaks: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
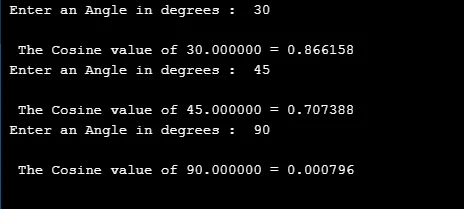
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Produksjon:
4. kosh ()
Den returnerer hyberbolisk kosinus for en gitt verdi.
syntaks:
double cosh(y);
Eksempel
Eksemplet nedenfor viser at det tar to forskjellige inndataverdier for å beregne hyperbol.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Produksjon

5. brunfarge ()
Denne matematiske bibliotekfunksjonen beregner tangensverdier for vinkelen for det matematiske uttrykket og målt i radianer.
Det kan erklæres som
double tan(arguments);
Eksempel
I den følgende kildekoden beregnes brunfargen for de følgende vinklene som økes med bruk for loop.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
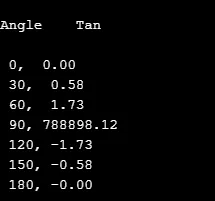
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Produksjon:
6. tanh ()
tanh () -funksjonen returnerer hyperbolsk tangens for den gitte verdien. Det tar en enkelt parameter. I tillegg til å finne tangens for lang dobbel og flytende tanhl () og tanhf () brukes til beregning.
syntaks:
double tanh( val);
Eksempel:
En tangent hyberbolic beregnes for 'j' verdier som brukes for løkker. La oss se hvordan det fungerer.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
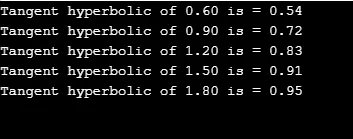
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Produksjon:
Log aritmetiske funksjoner
Nedenfor er de forskjellige funksjonene til log aritmetikk:
1. exp ()
Denne funksjonen beregner eksponentiell for en gitt verdi (e x ). Det er også andre undertyper som frexp (), Idexp () som returnerer mantissa og multiplisert til kraften til x.
syntaks:
return type exp(value);
Eksempel:
Programmet tar numerisk verdi fra brukeren for å beregne eksponenten for en gitt verdi og returnerer dobbelt.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Produksjon

2. logg ()
Denne funksjonen returnerer logaritmeverdien til et gitt nummer. (til basen e. log e )
syntaks:
double log(arg);
Eksempel:
I følgende eksempel beregnes loggverdien for det gitte tallet ved å bruke funksjon. Brukerdefinert funksjon lgm () gjør beregning og funksjon kalles i hovedfunksjonen.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
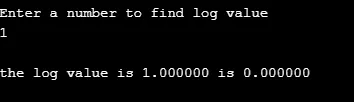
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
produksjon:
Konklusjon
For å konkludere, har vi sett forskjellige matematiske funksjoner som brukes i C-programmering, og dette er de direkte bibliotekfunksjonene som skal brukes. C-programmer bruker disse funksjonene for forskjellige matematiske operasjoner. For å løse noen komplekse versjoner av beregninger har denne innebygde funksjonen matematisk orientert programmeringsspråk til fordel for å returnere enkle verdier.
Anbefalte artikler
Dette er en guide til matematiske funksjoner i C. Her diskuterer vi forskjellige matematiske funksjoner i C med eksempler. Du kan også gå gjennom andre foreslåtte artikler -
- PHP matematiske funksjoner
- JavaScript-matematikkfunksjoner
- Overfør funksjoner i Matlab
- JavaScript-strengfunksjoner
- Introduksjon til matematiske funksjoner i Python
- Oversikt over matematiske funksjoner i C #
- C Programmering av matrixmultiplikasjon
- Square Root i PHP
- Eksempler på Square Root i JavaScript