
Bestemmelseskoeffisient Formel (Innholdsfortegnelse)
- Formel
- eksempler
Hva er bestemmelseskoeffisienten?
I statistikk er bestemmelseskoeffisient, også betegnet som R 2 et verktøy som bestemmer og vurderer evnen til en statistisk modell til å forklare og forutsi fremtidige resultater. Med andre ord, hvis vi har avhengig variabel y og uavhengig variabel x i en modell, hjelper R 2 med å bestemme variasjonen i y etter variasjon x. Det er en av nøkkelutgangene fra regresjonsanalyse og brukes når vi ønsker å forutsi fremtid eller teste noen modeller med relatert informasjon. Verdien av R2 ligger mellom 0 og 1 og høyere verdien på R2, bedre vil være prediksjonen og styrken til modellen. R2 er veldig lik korrelasjonskoeffisienten siden korrelasjonskoeffisienten måler direkte tilknytning av to variabler. R2 er i utgangspunktet et kvadrat av en korrelasjonskoeffisient.
Formel for bestemmelseskoeffisient:
Det er flere formler for å beregne bestemmelseskoeffisienten:
- Bruke korrelasjonskoeffisient:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Hvor:
- X - Datapunkter i datasett X
- Y - Datapunkter i datasett Y
- X m - Gjennomsnitt av datasett X
- Y m - Gjennomsnitt av datasett Y
Så
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Bruker regresjonsutganger
Bestemmelseskoeffisient (R 2 ) = Forklart variasjon / Total variasjon
Bestemmelseskoeffisient (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Hvor:
- TSS - Summen av kvadrater = Σ (Yi - Ym) 2
- MSS - Model Sum of Squares = Σ (Y - Ym) 2
- RSS - Rest sum av kvadrater = Σ (Yi - Y ^) 2
Y er den forutsagte verdien av modellen, Yi er ith-verdien og Ym er middelverdien
Eksempler på formel for bestemmelseskoeffisient (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av bestemmelseskoeffisienten på en bedre måte.
Du kan laste ned denne koeffisienten for bestemmelsesformel Excel-mal her - koeffisient for bestemmelsesformel Excel-malBestemmelseskoeffisient - Eksempel nr. 1
La oss si at vi har to datasett X & Y og hver inneholder 20 tilfeldige datapunkter. Beregn bestemmelseskoeffisienten for datasettet X & Y.
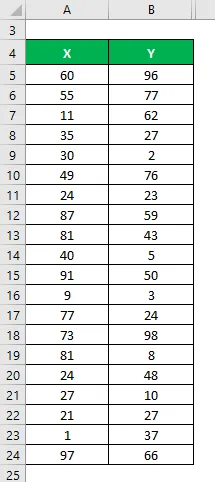
Gjennomsnitt beregnes som:
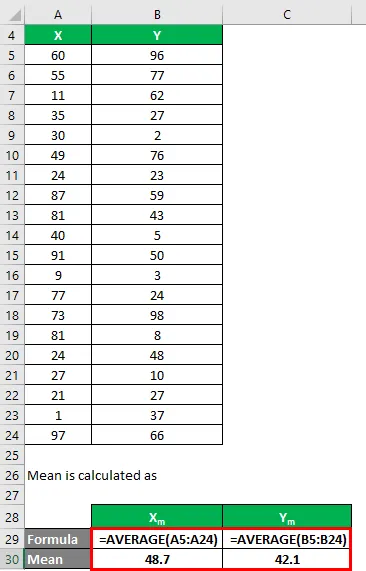
- Gjennomsnitt av datasett X = 48, 7
- Gjennomsnitt av datasett Y = 42.1
Nå må vi beregne forskjellen mellom datapunktene og middelverdien.
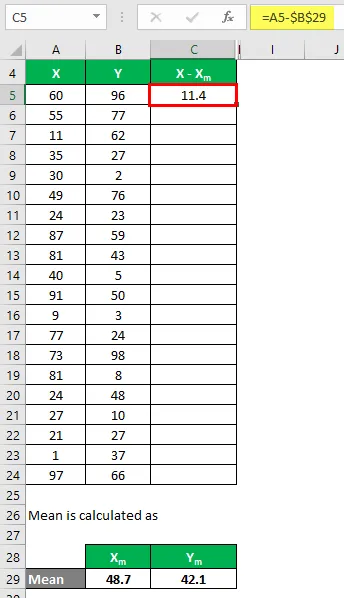
På samme måte beregner du for alle datasettet til X.
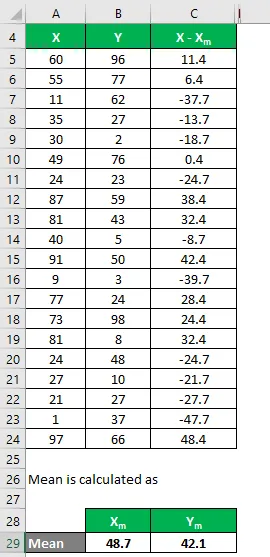
På samme måte kan du også beregne det for datasettet Y.

Beregn kvadratet av forskjellen for både datasettene X og Y.
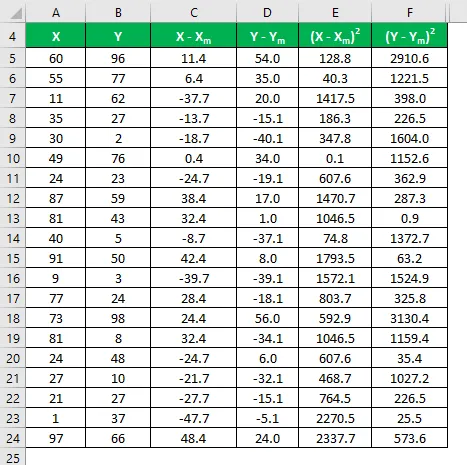
Multipliser forskjellen i X med Y.
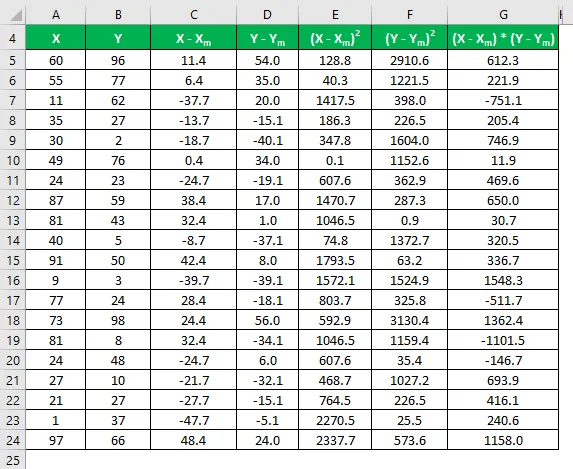
Korrelasjonskoeffisient beregnes ved å bruke formelen nedenfor
Korrelasjonskoeffisient = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
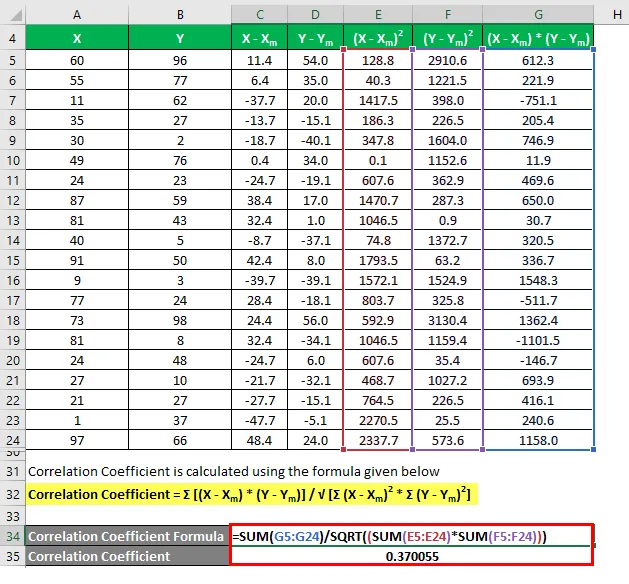
Bestemmelseskoeffisient beregnes ved å bruke formelen nedenfor
Bestemmelseskoeffisient = (korrelasjonskoeffisient) 2
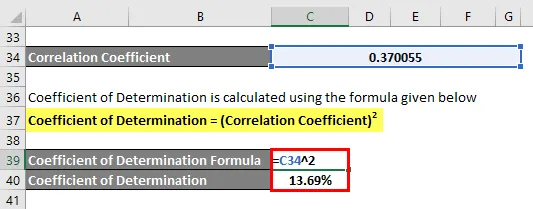
Bestemmelseskoeffisient = 13, 69%
Bestemmelseskoeffisient - Eksempel nr. 2
La oss si at du er en veldig risikovillig investor, og at du ønsker å investere penger i aksjemarkedet. Du er ikke sikker på hvilke aksjer du vil investere i, og risikoen for appetitten er også lav. Så du vil investere i en aksje som er trygg og som kan etterligne resultatene til indeksen. Din venn, som er en aktiv investor, har en liste på 3 aksjer for deg, basert på deres grunnleggende og tekniske informasjon, og du vil velge to aksjer blant disse tre.
Du har også samlet informasjon om historisk avkastning de siste 15 årene.
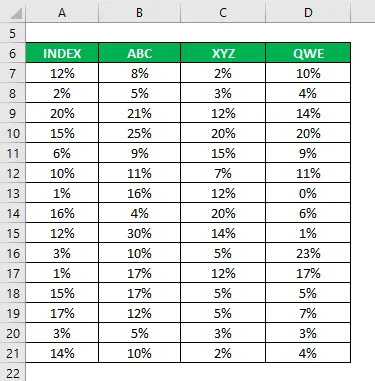
Korrelasjonskoeffisient beregnes ved å bruke excel-formelen
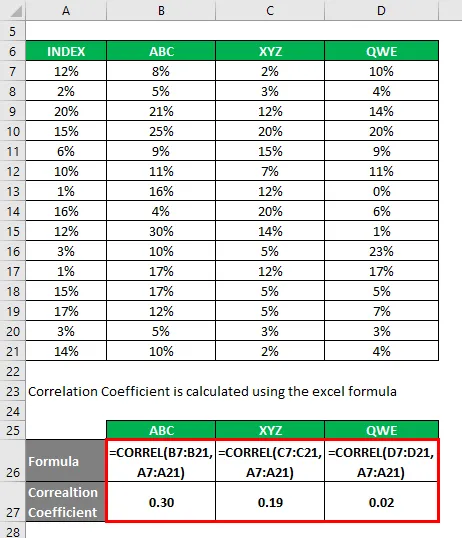
Bestemmelseskoeffisient beregnes ved å bruke formelen nedenfor
Bestemmelseskoeffisient = (korrelasjonskoeffisient) 2
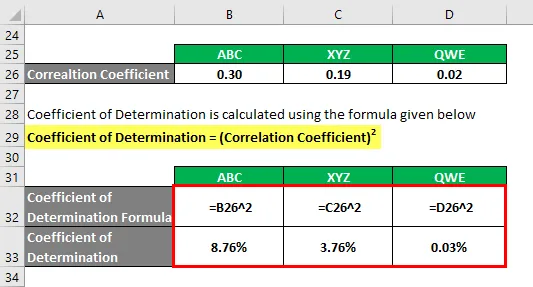
Basert på informasjonen, vil du velge aksje ABC og XYZ å investere siden de har den høyeste bestemmelseskoeffisienten.
Forklaring
Som forklart ovenfor er bestemmelseskoeffisienten kvadratet for korrelasjonen mellom to datasett. Hvis R2 er 0, betyr det at det ikke er noen korrelasjon og uavhengig variabel ikke kan forutsi verdien av den avhengige variabelen. Tilsvarende, hvis verdien er 1, betyr det at uavhengig variabel alltid vil være vellykket med å forutsi den avhengige variabelen. Men det er noen begrensninger også. Selv om det forteller oss korrelasjonen mellom to datasett, forteller den oss ikke om den verdien er nok eller ikke.
Stor verdi R2 innebærer ikke alltid at de to variablene har sterke relasjoner og det kan være en fluke. For eksempel: La oss si at R 2- verdien mellom et antall solgte biler i løpet av et år og antall iskremkasser som selges i løpet av et år er 80%. Men det er ingen sammenheng mellom disse to. Så man bør være veldig forsiktig når man bruker R 2 og forstå dataene først og deretter bruke metoden
Relevans og bruk av bestemmelseskoeffisientens formel
Det er mange praktiske anvendelser av R 2 . For eksempel er R2 veldig ofte brukt av investorer for å sammenligne resultatene til porteføljen deres med markedet og prøve å forutsi fremtidige retninger. På samme måte hjelper Hedge Funds R 2 dem med å modellere risikoen i modellene. Men til slutt er resultatet basert på rene tall og statistikker som kan være misvisende noen ganger. Som nevnt over, må man først sjekke om utgangen til R 2 gir mening i det virkelige liv eller ikke.
Anbefalte artikler
Dette har vært en guide til Formel for bestemmelse av koeffisient. Her diskuterer vi hvordan du beregner bestemmelseskoeffisienten sammen med praktiske eksempler og nedlastbar excel-mal. Du kan også se på følgende artikler for å lære mer -
- Guide to Premium Risk Formula
- Eksempler på dekningsforholdsformel
- Kalkulator for aktivitetsbasert beregningsformel
- Hvordan beregne informasjonsforhold ved bruk av formler?