
Sammensatt årlig veksthastighetsformel (Innholdsfortegnelse)
- Formel
- eksempler
- Kalkulator
Hva er den sammensatte årlige veksthastighetsformelen?
Compounding er effekten der en investering tjener renter ikke bare på hovedkomponenten, men også gir renter på renter. Så sammensatt årlig vekstrate er den effektive årlige veksten opptjent på investeringer med tanke på sammensetting i bildet. Dette forutsetter i utgangspunktet at rentene opptjent hvert år blir investert på nytt og at de tjener samme rente som hovedbeløpet. Det er grunnen til at sammensatt årlig vekstrate alltid er høyere enn enkelrenten. Mange investeringer som aksjefond, avkastning i aksjemarkedet er ikke veldig lineære og på en veldig ustabil måte.
Sammensatt årlig vekstrate hjelper til med å jevne ut avkastningen og vil fortelle hvor mye en investor har tjent i løpet av investeringstiden, gitt det faktum at alle inntektene mellom den perioden er reinvestert til samme takt. På grunn av denne jevnende effekten hjelper det oss å sammenligne datasett med ulikt volatilitetsnivå. Det brukes veldig ofte til finansiell analyse.
Avsluttende investeringsbeløp = Startbeløp (1 + CAGR) Antall år
Formelen for sammensatt årlig vekstrate -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Denne formelen er aktuelt hvis investeringen blir sammensatt årlig, betyr at vi investerer pengene på årsbasis. Men noen ganger hender det at vi ønsker å beregne hastigheten der sammensetningen skjer kvartalsvis, månedlig, daglig. Så for det bruker vi formelen nedenfor:
Avslutte investeringsbeløp = Startbeløp (1 + CAGR / sammensatt frekvens) (antall år * sammensatt frekvens)
Så, en formel for sammensatt årlig vekstrate -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Sammensatte frekvens:
- Semiannual Compounding: 2
- Kvartals sammensetning: 4
- Månedlig frekvens: 12 og så videre
Eksempler på CAGR-formler (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av CAGR-formelen på en bedre måte.
Du kan laste ned denne Compounded Annual Growth Rate Excel Template her - Compounded Annual Growth Rate Excel TemplateCAGR-formel - eksempel # 1
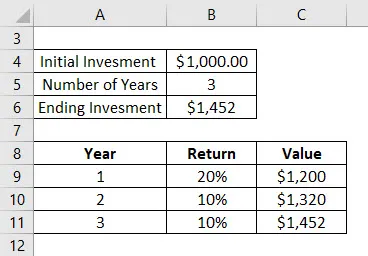
La oss si at du har investert 1000 dollar i aksjefond for 3 år siden. Følgende er avkastningen du har fått i disse tre årene:
- Det første året fikk du en verdiøkning på 20%. Så den totale verdien er $ 1200 ved slutten av det første året
- For andre år fikk du en verdiøkning på 10%. Så den totale verdien er $ 1320 ved utgangen av 2. året
- 3. året fikk du en verdiøkning på 10%. Så den totale verdien er $ 1452 ved utgangen av tredje året
CAGR beregnes ved å bruke formelen gitt nedenfor
CAGR = (Avsluttende investeringsbeløp / startbeløp) (1 / antall år) - 1
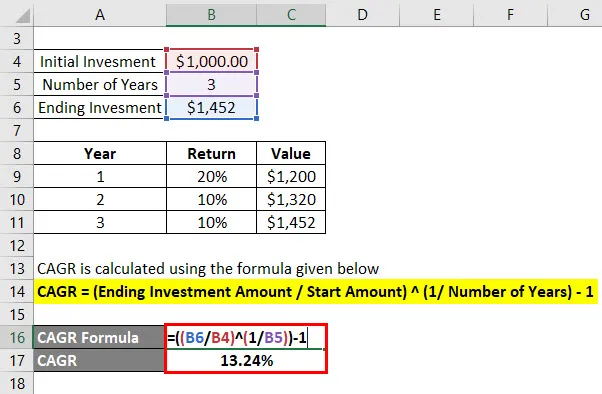
- CAGR = ($ 1 452 / $ 1 000) (1/3) - 1
- CAGR = 13, 24%
Her kan vi se at årlig avkastning for alle de tre årene er forskjellig og varierer, men den sammensatte årlige vekstraten gir oss en enkelt rente som vi kan sammenligne med forskjellige investeringsmuligheter.
CAGR-formel - eksempel # 2
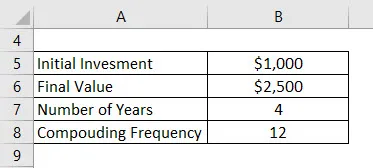
La oss si at du har investert 1000 dollar i banken og at du vil beholde pengene i banken i 4 år. La oss si at det totale beløpet du får etter 4 år er $ 2500. En bank tilbyr en rente med månedlig sammensetning. Beregn CAGR.
CAGR beregnes ved å bruke formelen gitt nedenfor
CAGR = sammensatt frekvens * ((avslutter investeringsbeløp / startbeløp) (1 / (antall år * sammensatt frekvens)) - 1)
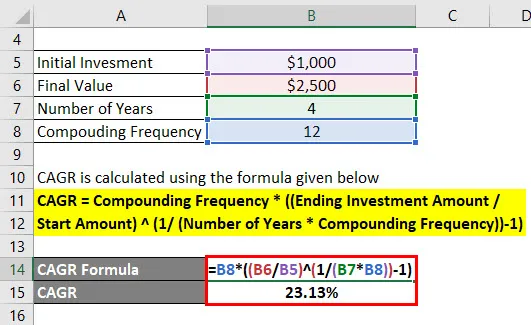
- CAGR = 12 * (($ 2500 / $ 1000) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Så sammensatt årlig vekstrate er 23, 13%.
Forklaring av sammensatt årlig veksthastighetsformel
Selv om den sammensatte årlige vekstraten er den årlige renten for investeringen, er den bare et teoretisk tall og er ikke den virkelige avkastningen. Den viktigste forutsetningen her er at alle inntektene blir reinvestert i samme takt for investeringsperioden, men satsen vil ikke forbli i alle år, og vi investerer kanskje ikke pengene våre i samme takt. Så det er en eneste representativ rente som forteller oss at det vi kan ende opp med hvis alle pengene blir investert på nytt i slutten av hvert år. Så det er noen viktige punkter som vi bør ta i betraktning mens vi bruker en sammensatt årlig vekstrate.
Vi vil også være veldig forsiktige med en investering som er lang. For eksempel, hvis en investeringsperiode er veldig lang, for eksempel 20 år, kan den sammensatte årlige renten gi oss feil indikasjon fordi det kan skje at vi ikke tjener noe overskudd i løpet av de første 15 årene, og all avkastning kommer i siste periode . Å tjene ingen fortjeneste i 15 år er ikke akseptabelt for noen virksomhet å opprettholde.
Tilsvarende, hvis to investeringsmuligheter har samme CAGR, kan det være slik at den ene er mer tiltrukket enn den andre på grunn av at veksten i den ene skjer i den innledende perioden, mens den for andre konsentreres mot slutten av periode.
Relevans og bruk av sammensatt årlig veksthastighetsformel
Den sammensatte årlige vekstraten er veldig nyttig i beregningen av den gjennomsnittlige vekstraten for investeringen og kan hjelpe med å sammenligne forskjellige investeringer. Som vi har sett i eksemplet ovenfor, er veksten i investeringene år til år ujevn og uberegnelig. Men ved bruk av sammensatt årlig vekstrate jevnes avkastningen ut. En annen faktor som gjør sammensatt årlig vekstrate til en kritisk metode for å bestemme veksten av en investering, er at den tar hensyn til sammensatt effekt, hvilken årlig avkastningsrate ikke. Sammensatt årsrente gir oss ikke det faktiske bildet av avkastningen, siden den bare beregner avkastningen på hovedbeløpet og ignorerer renten på rentekomponenten, men dette er ikke tilfelle med den sammensatte årlige vekstraten.
Sammensatt årlig vekstfrekvensformelberegner
Du kan bruke følgende sammensatte årlige veksttakskalkulator
| Avsluttende investeringsbeløp | |
| Start beløp | |
| Antall år | |
| CAGR | |
| CAGR = | ((Avsluttende investeringsbeløp / startbeløp) 1 / antall år -1) |
| = | ((0/0) 1/0 -1) = 0 |
Anbefalte artikler
Dette har vært en guide til sammensatt årlig veksthastighetsformel. Her diskuterer vi hvordan du beregner CAGR sammen med praktiske eksempler. Vi tilbyr også en sammensatt årlig vekstrate-kalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Guide to Rate of Return Formula
- Eksempler på eksponentiell vekstformel
- Kalkulator for formel for sentral begrensningsteorem
- Hvordan beregne markedsverdi?