
Variasjonskoeffisientformel (Innholdsfortegnelse)
- Formel
- eksempler
Hva er koeffisienten for variasjonsformel?
I statistikk er variasjonskoeffisienten også betegnet som CV et verktøy som hjelper oss å bestemme hvordan datapunkter i et datasett er fordelt rundt middelverdien. I utgangspunktet plottes alle datapunktene først, og deretter brukes variasjonskoeffisienten for å måle spredningen av disse punktene fra hverandre og middelverdien. Så det hjelper oss med å forstå dataene og også se mønsteret de danner. Det beregnes som et forhold mellom standardavviket til datasettet til middelverdi. Høyere variasjonskoeffisient betyr at det er et større spredningsnivå av data rundt middelverdien. Tilsvarende, lavere verdi av variasjonskoeffisienten, mindre er spredningen og mer presise vil være resultatene. Selv om gjennomsnittet for to dataserier er betydelig forskjellig, er variasjonskoeffisienten veldig nyttig for å sammenligne variasjonsgraden fra den ene dataserien til den andre.
Formel for variasjonskoeffisienten er gitt av:
Coefficient of Variation = Standard Deviation / Mean
Trinn for å beregne variasjonskoeffisienten:
Trinn 1: Beregn gjennomsnittet av datasettet. Gjennomsnitt er gjennomsnittet av alle verdiene og kan beregnes ved å ta summen av alle verdiene og deretter dele det med et antall datapunkter.
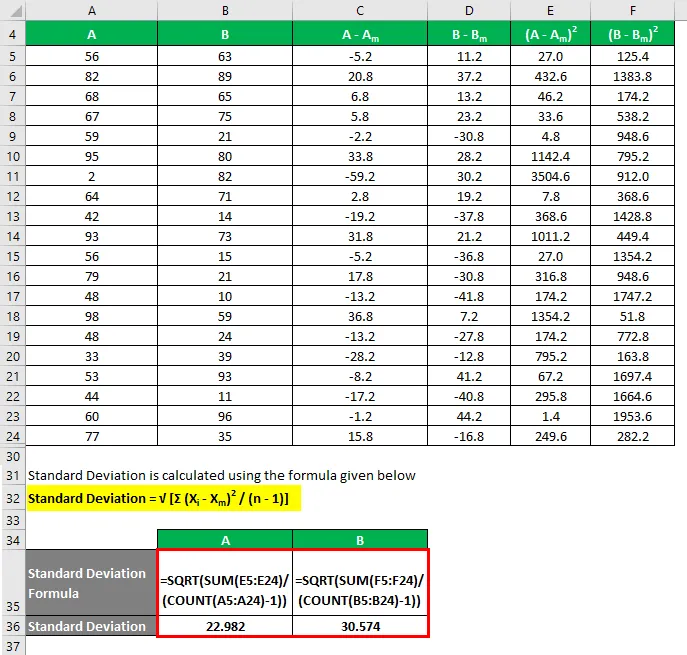
Trinn 2: Beregn deretter standardavviket for datasettet. Det er en litt tidkrevende prosess. Standardavvik kan beregnes som: √ (Σ (X i - X m ) 2 / (n - 1)) . X i er det datapunktet og X m er gjennomsnittet av datasettet. Alternativt kan vi også finne standardavviket i excel ved å bruke STDEV.S () -funksjonen.
Trinn 3: Del standardavvik med middel for å få variasjonskoeffisienten.
Eksempler på koeffisient for variasjonsformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av variasjonskoeffisienten på en bedre måte.
Du kan laste ned denne Koeffisient for Variation Formula Excel Template her - Coefficient of Variation Formula Excel TemplateVariasjonskoeffisientformel - Eksempel nr. 1
La oss si at vi har to datasett A & B, og hver inneholder 20 tilfeldige datapunkter. Beregn variasjonskoeffisienten for datasettet X & Y.
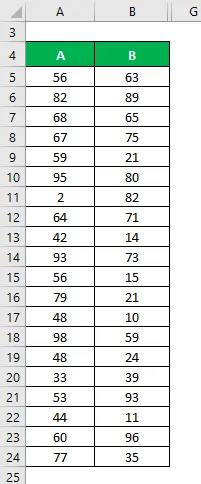
Løsning:
Gjennomsnitt beregnes som:
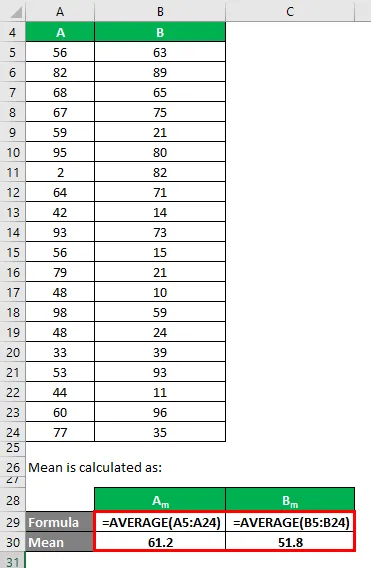
- Gjennomsnitt av datasett A = 61.2
- Gjennomsnitt av datasett B = 51, 8
Nå må vi beregne forskjellen mellom datapunktene og middelverdien.
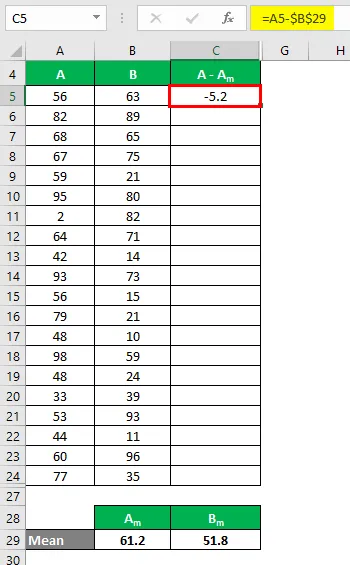
Beregn på samme måte for alle verdiene til datasettet A.
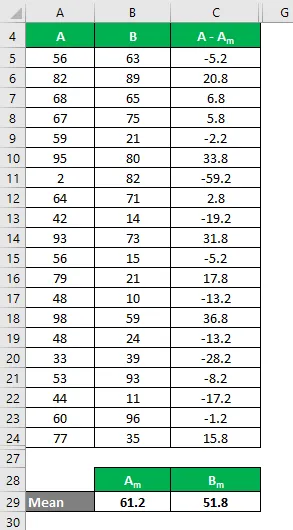
Beregn på samme måte for alle verdiene i datasettet B.
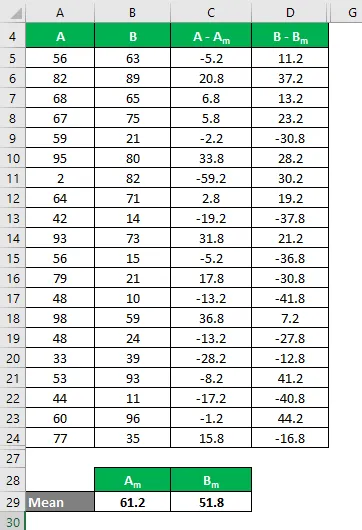
Beregn kvadratet av forskjellen for både datasettene A og B.
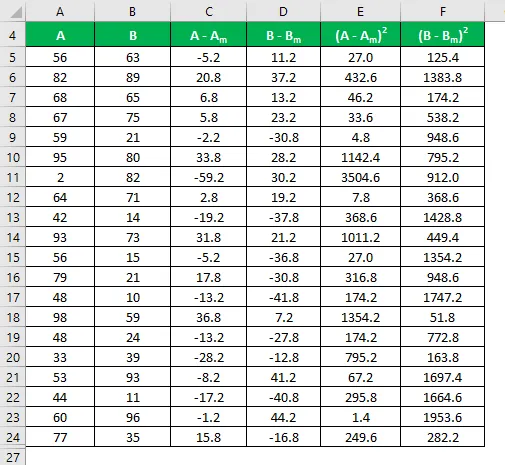
Standardavvik beregnes ved å bruke formelen gitt nedenfor
Standardavvik = √ (Σ (X i - X m ) 2 / (n - 1))
Variasjonskoeffisient beregnes ved å bruke formelen nedenfor
Variasjonskoeffisient = standardavvik / middel
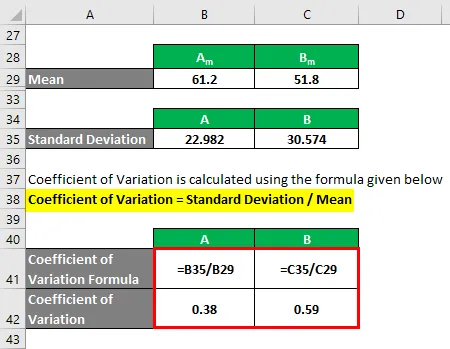
- Variasjonskoeffisient A = 22.982 / 61.2 = 0.38
- Variasjonskoeffisient B = 30, 574 / 51, 8 = 0, 59
Så hvis du ser her, har B en høyere variasjonskoeffisient enn A, noe som betyr at datapunktene til B er mer spredt enn A.
Variasjonskoeffisientformel - eksempel # 2
La oss si at du er en veldig risikovillig investor, og at du ønsker å investere penger i aksjemarkedet. Siden risikovilligheten din er lav, vil du investere i trygge aksjer som har lavere standardavvik og variasjonskoeffisient. Du har listet tre aksjer basert på grunnleggende og teknisk informasjon og vil velge to aksjer. Du har også samlet informasjon om historisk avkastning de siste 15 årene.
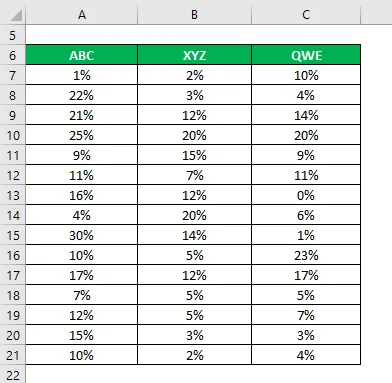
Løsning:
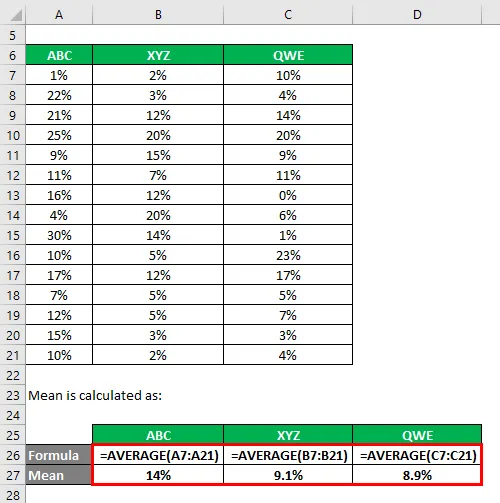
Gjennomsnitt beregnes som:
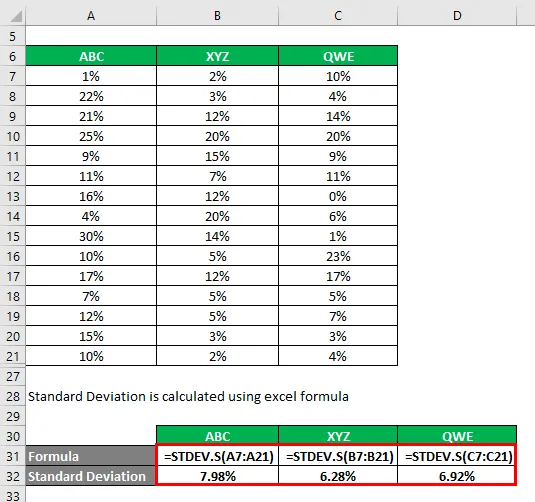
Standardavvik beregnes ved å bruke excel-formel
Variasjonskoeffisient beregnes ved å bruke formelen nedenfor
Variasjonskoeffisient = standardavvik / middel
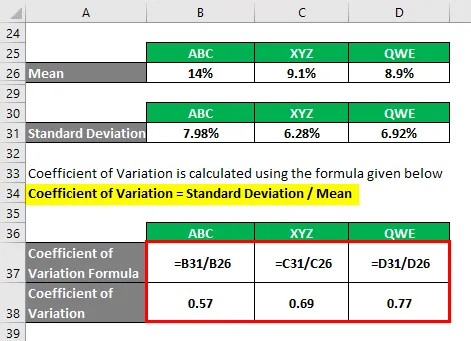
- Variasjonskoeffisient ABC = 7, 98% / 14% = 0, 57
- Variasjonskoeffisient XYZ = 6, 28% / 9, 1% = 0, 69
- Variasjonskoeffisient QWE = 6, 92% / 8, 9% = 0, 77
Basert på informasjonen, vil du velge aksje ABC og XYZ å investere siden de har den laveste variasjonskoeffisienten.
Forklaring
Siden variasjonskoeffisienten er et mål på risiko, hjelper det med å måle volatiliteten i prisene på aksjer og andre finansielle instrumenter. Det hjelper også investorer og analytikere med å sammenligne risikoen forbundet med forskjellige potensielle investeringer.
Variasjonskoeffisient er lik standardavvik, men et standardavvik for to variabler kan ikke sammenlignes i nyttige. Men å bruke standardavvik og middelverdien gjør den relative sammenligningen mer meningsfull. Det er en begrensning av variasjonskoeffisienten også. Anta at gjennomsnittet av et datasett er null. I så fall vil dette verktøyet bli ineffektivt. Ikke bare dette, hvis vi har et datasett som har mange positive og negative verdier, blir variasjonskoeffisienten veldig problematisk. Så det er bare mer nyttig når datasett har samme pluss-minus-tegn.
Relevans og bruk av formel for variasjonskoeffisient
Variasjonskoeffisient har relevans på mange andre felt enn statistikk. For eksempel innen finansfeltet, er variasjonskoeffisienten et mål på risiko. Det ligner standardavvik, siden det også brukes som et mål på risiko, men forskjellen er at variasjonskoeffisienten er en bedre indikator på relativ risiko. La oss for eksempel si As forventede avkastning på 15% og Bs forventede avkastning på 10% og A har et standardavvik på 10%, mens B har et standardavvik på 5%. For å velge en bedre investering kan variasjonskoeffisienten brukes. Så variasjonskoeffisienten av A er 10/15 = 0, 666 og variasjonskoeffisienten av B er 5/10 = 0, 5. Så B er en bedre investering enn A.
Anbefalte artikler
Dette har vært en guide til Formel av koeffisient for variasjon. Her diskuterer vi hvordan du beregner variasjonskoeffisienten ved å bruke formel sammen med praktiske eksempler og nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Hva er justert R-kvadratformel?
- Eksempler på koeffisient for bestemmelsesformel
- Hvordan beregne korrelasjonskoeffisienten ved å bruke formler?
- Covariance-formel med Excel-mal