
F-testformel (innholdsfortegnelse)
- Formel
- eksempler
Hva er F-testformel?
F-test er en statistisk test som hjelper oss med å finne om to populasjonssett som har en normal fordeling av datapunktene har samme standardavvik eller avvik. Men den første og fremste tingen å utføre F-test er at datasettene skal ha en normal fordeling. Dette brukes på F-distribusjon under nullhypotesen. F-test er en veldig viktig del av analysen av variasjon (ANOVA) og beregnes ved å ta forholdstall mellom to varianser av to forskjellige datasett. Som vi vet at avvik gir oss informasjonen om spredning av datapunktene. F-test brukes også i forskjellige tester som regresjonsanalyse, Chow-testen, etc.
Formel FOR F-Test:
Det er ingen enkel formel for F-Test, men det er en serie trinn som vi må følge:
Trinn 1: For å utføre en F-test, må vi først definere nullhypotesen og alternativ hypotesen. Disse er gitt av: -
- H0 (Null hypotese): Variasjon av 1. datasett = Variasjon av et 2. datasett
- Ha: Variasjon av 1. datasett <Variasjon av 2. datasett (for en lavere en-tailed test)
- Ha: Variasjon av 1. datasett> Variasjon av et 2. datasett (for en øvre en-tailed test)
- Ha: Variasjon av 1. datasett ≠ Variasjon av et annet datasett (for en test med to tetall)
Trinn 2: Neste ting vi må gjøre er at vi trenger å finne ut hvilken grad av betydning og deretter bestemme frihetsgrader for både teller og nevner. Dette hjelper oss med å bestemme kritiske verdier. Frihetsgrad er utvalg størrelse -1.
Trinn 3: F-testformel:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Trinn 4: Finn F-kritiske verdien fra F-tabellen med en grad av frihet og nivå av betydning.
Trinn 5: Sammenlign disse to verdiene, og hvis en kritisk verdi er mindre enn F-verdien, kan du avvise nullhypotesen.
Eksempler på F-testformler (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av F-Test på en bedre måte.
Du kan laste ned denne F-TEST-formelen Excel-malen her - F-TEST-formelen Excel-malenF-testformel - eksempel # 1
La oss si at vi har to datasett A & B som inneholder forskjellige datapunkter. Utfør F-test for å avgjøre om vi kan avvise nullhypotesen på 1% nivå av betydning.
Datasett:
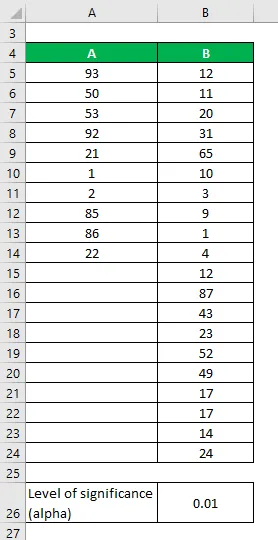
Løsning:
Nullhypotese: Variance of A = Variance of B
Grad of Freedom beregnes som
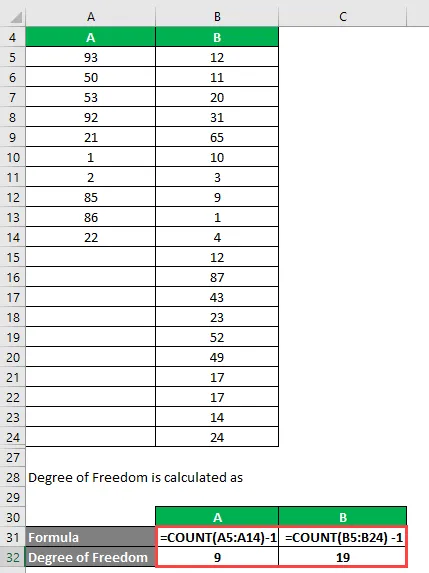
Grad av frihet
- For A = 10 - 1 = 9
- For B = 20 - 1 = 19
Variasjonen beregnes som:

- Varians av A = 1385, 61
- Varians av B = 521, 22
F Verdi beregnes ved å bruke formelen nedenfor
F Verdi = variant av 1. datasett / variant av 2. datasett
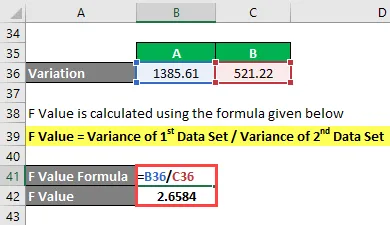
- F-verdi = 1385, 61 / 521, 22
- F verdi = 2.6584
F-tabell:
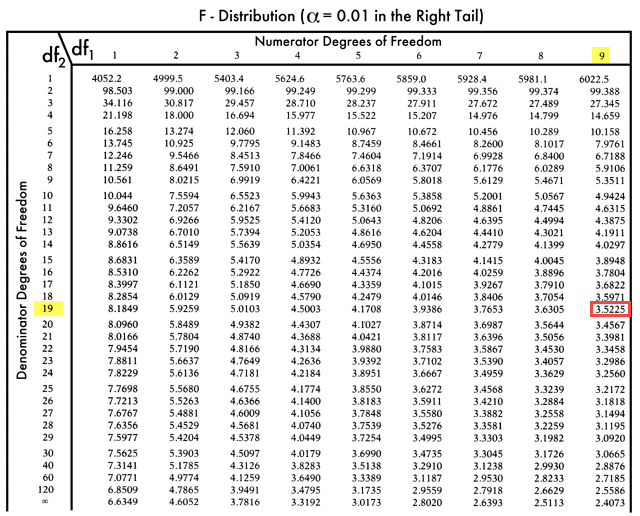
Altså F kritisk verdi = 3.5225
Siden F critical er større enn F-verdien, kan vi ikke avvise nullhypotesen.
F-testformel - eksempel # 2
Anta at du jobber i et forskningsfirma og vil at nivået av karbonoksidutslipp skjer fra to forskjellige merker sigaretter, og om de er vesentlig forskjellige eller ikke. I analysen din har du samlet følgende informasjon:
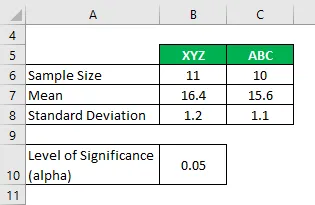
Løsning:
Grad of Freedom beregnes som
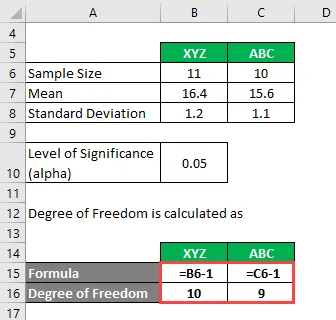
Grad av frihet
- For XYZ = 11 - 1 = 10
- For ABC = 10 - 1 = 9
Variasjonen beregnes som:
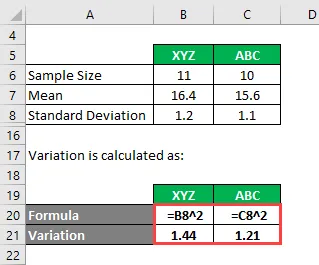
- Varians av XYZ = 1, 2 2 = 1, 44
- Varians av ABC = 1, 1 2 = 1, 21
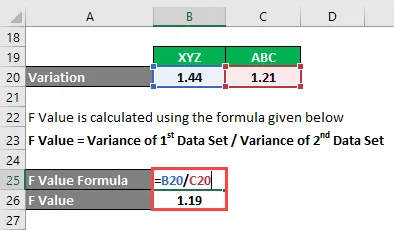
- F-verdi = 1, 44 / 1, 21
- F-verdi = 1, 19
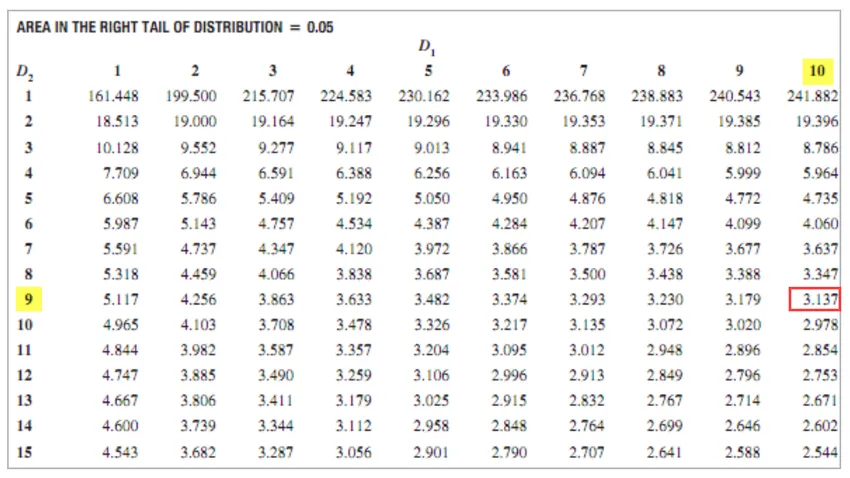
F Kritisk verdi = 3.137
Siden F-kritisk> F-verdi, kan ikke nullhypotesen avvises.
Forklaring
I eksemplene over har vi sett anvendelsen av F-Test og hvordan den blir utført. Men det er et sett med antakelser vi må passe på før vi utfører F-Test, ellers får vi ikke nødvendige resultater:
- Det første er at vi alltid må plassere telleren for høyere variansverdi mens vi beregner F-verdien. Så hvis F = V1 / V2, bør V1 være> V2
- Hvis vi ønsker å utføre 2 haletest, må vi dele betydningsnivået med 2 og det vil være riktig nivå for å finne den kritiske verdien
- Vi bruker bare varians er F-verdiberegningen, og hvis vi er gitt med standardavvik, som i eksempel 2, må de være kvadrat for å finne variansen.
- Begge prøvene skal være uavhengige av hverandre og prøvestørrelsen skal være mindre enn 30
- Befolkningssett hvor prøvene blir trukket ut må normalt distribueres
Dette er de viktigste parameterne / antakelsen som bør tas vare på mens du utfører F-Test.
Relevans og bruk av F-testformler
F-Test, som diskutert over, hjelper oss å sjekke om likheten mellom de to befolkningsavvikene er. Så når vi har to uavhengige prøver som er hentet fra en normal populasjon og vi vil sjekke om de har samme variabilitet eller ikke, bruker vi F-test. F-test har også stor relevans i regresjonsanalyse og også for testing av betydningen av R2. Så i et nøtteskall, er F-Test et veldig viktig verktøy i statistikk hvis vi vil sammenligne variasjonen av to eller flere datasett. Men man bør huske alle forutsetningene før man utfører denne testen.
Anbefalte artikler
Dette har vært en guide til F-Test Formula. Her diskuterer vi hvordan du beregner F-Test sammen med praktiske eksempler og nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- T Distribusjonsformel
- Formel for prissetting av obligasjoner
- Prosentfeilformel
- Beregning av NOPAT-formelen