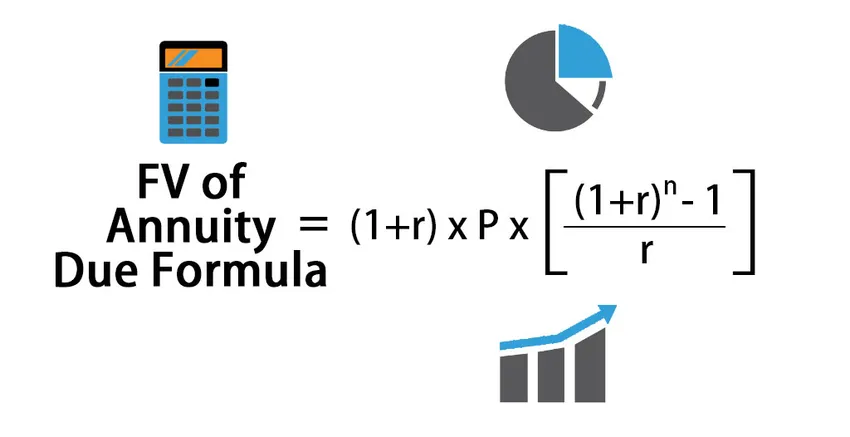
Future Value of Annuity Due Formula (Innholdsfortegnelse)
- Future Value of Annuity Due Formula
- Eksempler på fremtidig verdi av formel for livrente (med Excel-mal)
- Framtidig verdi av kalkulator for annuitet grunn formel
Future Value of Annuity Due Formula
Formelen for beregning av Future Value of Annuity Due:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Hvor,
- P = Periodisk betaling
- R = Rente per periode
- N = Antall perioder
Eksempler på fremtidig verdi av formel for livrente (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av Future Value of Annuity Due på en bedre måte.
Du kan laste ned denne Future Value of Annuity Due Formula Excel Template her - Future Value of Annuity Due Formula Excel TemplateEksempel 1
La oss anta at en Anand har satt inn $ 10.000 per år og den effektive satsen hans konto tilbyr er 3%. Nå ønsker Anand å beregne sin fremtidige saldo etter 5 år med å anta første innskudd fra i dag og fremover.
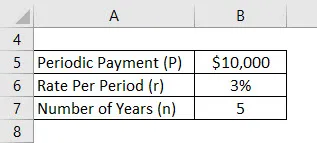
Løsning:
Future Value of Annuity Due beregnes ved å bruke formelen nedenfor
FV of Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
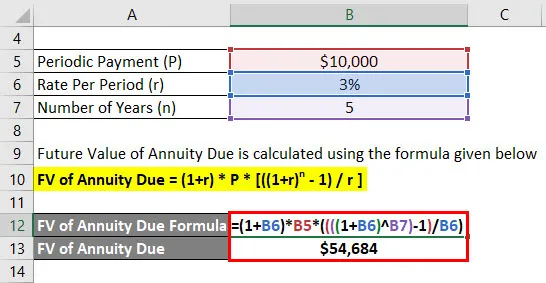
- FV of Annuity Due = (1+ 3%) * $ 10.000 * (((((1 + 3%) 5) - 1) / 3%)
- FV of Annuity Due = $ 54.684
Anand vil få $ 54, 684 fremtidig saldo etter 5 år.
Eksempel 2
La oss anta at en Jagriti har satt inn $ 8000 per år og den effektive satsen hans konto tilbyr er 5%. Nå ønsker Jagriti å beregne sin fremtidige saldo etter 5 år med å anta første innskudd fra i dag og fremover.

Løsning:
Future Value of Annuity Due beregnes ved å bruke formelen nedenfor
FV of Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
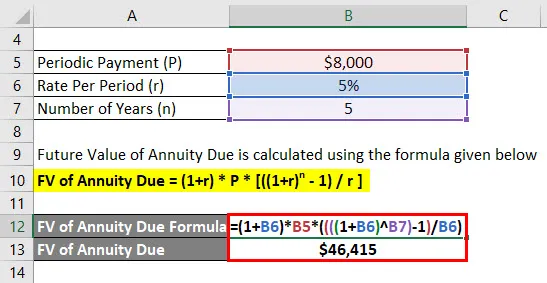
- FV of Annuity Due = (1+ 5%) * $ 8000 * (((((1 + 5%) 5) - 1) / 5%)
- FV of Annuity Due = $ 46.415
Jagriti vil få $ 46.415 fremtidig saldo etter 5 år.
Eksempel 3
La oss anta at en Anandriti har satt inn $ 20 000 per år og den effektive satsen hans konto tilbyr er 2%. Nå ønsker Anandriti å beregne sin fremtidige saldo etter 5 år med å anta første innskudd fra i dag og fremover.
Løsning:
Future Value of Annuity Due beregnes ved å bruke formelen nedenfor
FV of Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
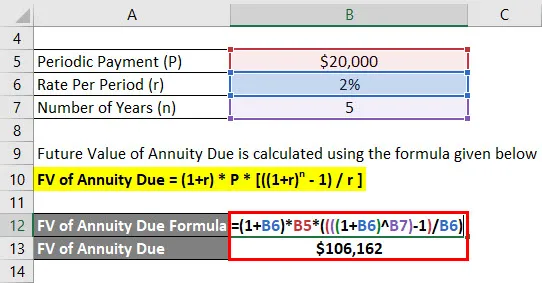
- FV of Annuity Due = (1+ 2%) * $ 20.000 * (((((1 + 2%) 5) - 1) / 2%)
- FV of Annuity Due = $ 1.06.162
Anandriti vil få $ 1.06.162 fremtidig saldo etter 5 år.
Forklaring
For å beregne sluttverdien for en serie med kontantstrømmer eller betaling der den første avbetalingen mottas øyeblikkelig, bruker vi Future Value of annuity. Den første øyeblikkelige avbetalingen eller betalingen skiller livrenten på grunn av den ordinære livrenten. En øyeblikkelig eller øyeblikkelig livrente blir referert til som en forfalt livrente.
Den beregner verdien av kontantstrømmer i en fremtidig periode. Bruken av FV på forfalt livrente er annerledes i reelle situasjoner enn nåverdien av en forfalt livrente. Anta for eksempel at et selskap eller en person kjøper en livrente og har betalt det første avdraget i dag. Vi kan bruke eksemplet til å forklare videre, anta at et selskap eller en person ønsker å kjøpe en livrente fra noen og har utført den første betalingen i dag. For å beregne prisen som skal betales i denne situasjonen, kan vi bruke nåverdien av livrenteformelen. Imidlertid, hvis vi ønsker å beregne den gjenværende saldoen etter å ha spart renter i 5 år på kontoen og vi bestemte oss for å betale den første avdrag i dag, brukes i dette tilfellet den fremtidige verdien av en annuitet. Forfalte livrente kan forklares som en type livrente hvor kontantstrømmer oppstår ved starten av hver periode. På grunn av den avanserte arten av kontantstrømmer, er hver kontantstrøm underlagt den sammensatte effekten for hver ekstra periode i tilfelle den sammenlignes med en ordinær livrente. Den fremtidige verdien av en ordinær livrente er lavere enn den fremtidige verdien av livrenten, ettersom den fremtidige verdien av livrenten får en periodisk rente på faktoren ett pluss.
Relevans og bruk av fremtidig verdi av forfalt livrente
La oss forstå betydningen av fremtidig verdi og livrente separat. Framtidig verdi kan forklares som den totale verdien for en sum kontanter som skal betales fremover på en bestemt dato. Og en forfalt livrente kan forklares som den innbetalingsserie som gjøres i begynnelsen av hver periode i vanlig rekkefølge. Derfor kan fremtidig forrentningsgevinst forklares som den totale verdien på en spesifikk dato i fremtiden for en serie systematisk / periodisk betaling der betalingene skjer i begynnelsen av hver periode. Denne typen transaksjoner og en slik strøm av utbetalinger kan sees på en mottakerkonto for en pensjonsplan. Den totale verdien er beløpet som serien av utbetalinger som blir gjort fremover vil vokse til, ettersom det antas en viss rente, og inntektene øker gradvis over en viss periode. Beregningen av fremtidig verdi av en ordinær livrente er identisk med denne, men den eneste forskjellen er at vi legger til en ekstra betalingsperiode som gjøres i begynnelsen.
Framtidig verdi av kalkulator for annuitet grunn formel
Du kan bruke følgende Future Value of Annuity Due Calculator
| P | |
| r | |
| n | |
| Future Value of Annuity Due Formula | |
| Future Value of Annuity Due Formula = | (1 + r) * P * ((((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Anbefalte artikler
Dette har vært en guide til Future Value of Annuity Due Formula. Her diskuterer vi hvordan du beregner Future Value of Annuity Due sammen med praktiske eksempler. Vi tilbyr også Future Value of Annuity Due kalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Veiledning for formel for tidsverdi av penger
- Eksempler på nåverdier faktorformler
- Kalkulator for informasjonsforholdsformel
- Formel for grad av driftsmakt