
Introduksjon til eksempler på standardavvik
Det er mange eksempler på standardavvik. Standardavvik er mål på spredning av datasett, dvs. hvor spredte tallene er. Det er nyttig å sammenligne de forskjellige datasettene som kan ha samme gjennomsnitt, men det forskjellige området. Følgende forskjellige standardavvikseksempel gir forståelse for den vanligste situasjonstypen der standardavviket beregnes og hvordan man kan beregne det samme
Eksempler på standardavvik
Nedenfor er eksemplene på standardavviket
Standardavvik - eksempel # 1
Aksjen i Company Z selger for $ 50 per aksje og de samme tilbudene etter utbetalinger for det neste året:
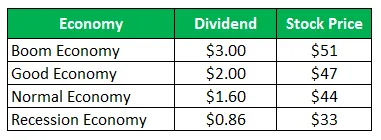
Beregn standardavviket når alle de fire scenariene er gitt er like sannsynlige.
Løsning:
Beregninger av tilbakeholdelse av periode (HPR) er som følger -
Formel for HPR
HPR = ((Periodens sluttverdi - originalverdi) + inntekt) / originalverdi) * 100
For Boom Economy
- HPR (Boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (Bra) = ((47-50) + 2) / 50 = -2, 00%
- HPR (Normal) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (resesjon) = ((33-50) + 0, 86) / 50 = -32, 28%
Beregning av forventet avkastning
Siden alle scenariene er like sannsynlige, vil sannsynligheten for alle være ¼
Formel for forventet retur
Forventet retur = (sannsynlighet for bom * retur fra bom) + (sannsynlighet for god * retur fra god) + (sannsynlighet for normal * retur fra normal) + (sannsynlighet for resesjon * retur fra resesjon)
- Forventet avkastning = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Forventet avkastning = -8, 77%
Beregning av standardavvik
Formel of Variance
Varians = (Probability of Boom * (Return from Boom - Total Expected Return) 2) + (Probability of Good * (Return from Good - Total Expected Return) 2) + (Probability of Normal * (Return from Normal - Total Expected Return) 2 ) + (sannsynlighet for resesjon * (retur fra resesjon - total forventet retur) 2)
- Varians = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varians = 219, 95
Formel for standardavvik
Standardavvik vil være Square Root of Variance
Standardavvik = √ Variasjon
- Standardavvik = 219, 95
- Standardavvik = 14, 83%
Standardavvikseksempel - 2
Standardavvik for to selskaper i porteføljen
Den vanlige aksjen i selskapet A selger for $ 28 per aksje og de samme tilbudene etter utbetalinger for det neste året

Den vanlige aksjen i selskap B selger for $ 93 per aksje og de samme tilbudene etter utbetalinger for det neste året:

(a) Beregn standardavviket til firma A
(b) Beregn standardavviket til firma B
(c) Beregn porteføljens standardavvik hvis halvparten av investeringen gjøres er selskap A og resten halvparten av selskap B
Løsning:
For selskap A
Beregninger av tilbakeholdelse av periode (HPR)
Formel for HPR
HPR = ((Periodens sluttverdi - originalverdi) + inntekt) / originalverdi) * 100
- HPR (bom) = ((20-28) + 1) / 28 = -25, 00%
- HPR (Normal) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (resesjon) = ((38-28) + 5) / 28 = 53, 57%
Beregning av forventet avkastning av selskap A
Formel for forventet retur
Forventet retur = (sannsynlighet for bom * retur fra bom) + (sannsynlighet for normal * retur fra normal) + (sannsynlighet for resesjon * retur fra resesjon)
- Forventet avkastning = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Forventet avkastning = 3, 84%
Beregning av standardavviksselskap A
Formel of Variance
Varians = (sannsynlighet for bom * (retur fra bom - samlet forventet avkastning) 2) + (sannsynlighet for normal * (retur fra normal - samlet forventet avkastning) 2 ) + (sannsynlighet for resesjon * (retur fra resesjon) - samlet forventet avkastning) 2)
- Varians = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varians = 895, 15
Formel for standardavvik
Standardavvik vil være Square Root of Variance
Standardavvik = √ Variasjon
- Standardavvik = √ 895.15
- Standardavvik = 29, 92%
For firma B
Beregninger av tilbakeholdelse av periode (HPR)
Formel for HPR
HPR = ((Periodens sluttverdi - originalverdi) + inntekt) / originalverdi) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122, 58%
HPR (Normal) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (resesjon) = ((4-93) +2) / 93 = -93, 55%
Beregning av forventet avkastning
Formel for forventet retur
Forventet retur = (sannsynlighet for bom * retur fra bom) + (sannsynlighet for normal * retur fra normal) + (sannsynlighet for resesjon * retur fra resesjon)
- Forventet avkastning = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Forventet avkastning = 43, 04%
Beregning av standardavvik
Formel of Variance
Varians = (sannsynlighet for bom * (retur fra bom - samlet forventet avkastning) 2) + (sannsynlighet for normal * (retur fra normal - samlet forventet avkastning) 2 ) + (sannsynlighet for resesjon * (retur fra resesjon) - samlet forventet avkastning) 2)
- Varians = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varians = 6783, 65
Formel for standardavvik
Standardavvik vil være Square Root of Variance
Standardavvik = √ Variasjon
- Standardavvik = √6783.65
- Standardavvik = 82, 36%
Beregning av forventet avkastning og standardavvik for en portefølje halvparten investert i selskap A og halvparten i selskap B.
Standardavvik for selskap A = 29, 92%
Standardavvik for selskap B = 82, 36%
Vekt av selskap A = 0, 50
Vekt av selskap B = 0, 50
Formelen for Standard Deviation of Portfolio
Standardavvik for portefølje = (Vekt av selskap A * Forventet avkastning av selskap A) + ((Vekt av selskap B * Forventet avkastning av selskap B)
- Standardavvik for portefølje = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standard avvik for portefølje = 56, 14%
Analyse
Porteføljens standardavvik er lavere enn for begge aksjers individ fordi aksjene er diversifisert i forskjellige aksjer. Diversifisering fører til reduksjon i risikoen med mindre det er en perfekt sammenheng mellom avkastningen på porteføljeinvesteringer.
Konklusjon - Standardavvikseksempler
Standardavviket måler spredningen av datasettet som er relativt til dets gjennomsnitt. Det beregnes som kvadratroten av varians. Jo større standardavviket for sikkerheten er, desto større vil variansen mellom hver pris og middelverdi være, noe som viser at prisklassen er stor. Ovennevnte eksempler er noen av eksemplene på standardavvik på forskjellige måter. Det er forskjellige andre eksempler som viser at standardavvik kan beregnes ved bruk av andre data.
Anbefalte artikler
Dette har vært en guide til standardavvikseksemplene. Her diskuterer vi de forskjellige eksemplene på standardavvik sammen med en detaljert forklaring . Du kan også se på følgende artikler for å lære mer -
- Faste kostnader Eksempel
- Eksempel på variabel kostnad
- Kvantitativt eksempel
- Eksempler på monopolistiske konkurranser