
Margin of Error Formula (Innholdsfortegnelse)
- Margin of Error Formula
- Eksempler på margin av feilformel (med Excel-mal)
- Marginal of Error Formula Calculator
Margin of Error Formula
I statistikk beregner vi konfidensintervallet for å se hvor verdien av dataene til prøvestatistikk vil falle. Verdiene som ligger under og over prøvestatistikken i et konfidensintervall er kjent som Margin of Error. Det er med andre ord i utgangspunktet feilgraden i utvalgsstatistikken. Høyere feilmargin, jo mindre vil tilliten til resultatene være, fordi graden av avvik i disse resultatene er veldig høy. Som navnet antyder, er feilmarginen et område med verdier over og under de faktiske resultatene. For eksempel, hvis vi får svar i en undersøkelse der 70% mennesker har svart "bra" og feilmargin er 5%, betyr dette at 65% til 75% av befolkningen generelt mener at svaret er "godt" .
Formelen for Margin of Error -
Margin of Error = Z * S / √n
Hvor:
- Z - Z score
- S - Standardavvik for en befolkning
- n - Prøvestørrelse
En annen formel for beregning av feilmarginen er:
Margin of Error = Z * √((p * (1 – p)) / n)
Hvor:
- p - Eksempel Andel (brøkdel av prøven som er en suksess)
Nå for å finne ønsket z-poengsum, må du kjenne til konfidensintervallet til prøven fordi Z-poengsummen er avhengig av den. Under tabellen er gitt for å se forholdet mellom et konfidensintervall og z-poengsum:
| Konfidensintervall | Z - Poeng |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1.96 |
| 99% | 2, 58 |
Når du har fått vite konfidensintervallet, kan du bruke den tilsvarende z-verdien og beregne feilmarginen derfra.
Eksempler på margin av feilformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av Margin of Error på en bedre måte.
Du kan laste ned denne Margin of Error Mal her - Margin of Error TemplateMargin of Error Formula - Eksempel # 1
La oss si at vi gjennomfører en undersøkelse for å se hva karakteren som universitetsstudentene får er. Vi har valgt 500 elever tilfeldig og bedt karakteren deres. Gjennomsnittet av dette er 2, 4 av 4 og standardavviket er si 30%. Anta at konfidensintervallet er 99%. Beregn feilmarginen.
Løsning:
Feilmargin beregnes ved å bruke formelen nedenfor
Feilmargin = Z * S / √n
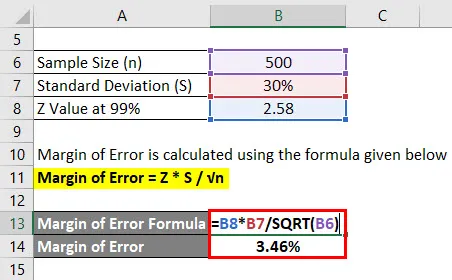
- Feilmargin = 2, 58 * 30% / √ (500)
- Feilmargin = 3, 46%
Dette betyr at med 99% selvtillit er gjennomsnittlig karakter av studentene 2, 4 pluss eller minus 3, 46%.
Margin of Error Formula - Eksempel # 2
La oss si at du lanserer et nytt helseprodukt i markedet, men du er forvirret hvilken smak som folk vil like. Du er forvirret mellom banansmak og vaniljesmak og har bestemt deg for å gjennomføre en undersøkelse. Befolkningen din for det er 500 000 som er ditt målmarked, og ut av det bestemte du deg for å spørre mening om 1000 mennesker, og det vil utvalget. Anta at et konfidensintervall er 90%. Beregn feilmarginen.
Løsning:
Når undersøkelsen er gjort, ble du kjent med at 470 personer likte banansmaken og 530 har bedt om vaniljesmak.
Feilmargin beregnes ved å bruke formelen nedenfor
Feilmargin = Z * √ ((p * (1 - p)) / n)
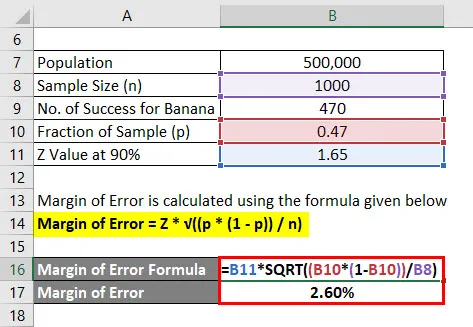
- Feilmargin = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Feilmargin = 2, 60%
Så vi kan si det med 90% tillit til at 47% av alle mennesker likte banansmak pluss eller minus 2, 60%.
Forklaring
Som diskutert ovenfor, hjelper feilmarginen oss med å forstå om utvalgsstørrelsen til undersøkelsen din er passende eller ikke. I tilfelle marginfeilen er for stor, kan det være slik at utvalgsstørrelsen vår er for liten, og vi må øke den slik at utvalgsresultatene samsvarer tettere med bestandsresultatene.
Det er noen scenarier der feilmarginen ikke vil være til stor nytte og ikke hjelper oss med å spore feilen:
- Hvis spørsmålene til undersøkelsen ikke er utformet og ikke hjelper med å få ønsket svar
- Hvis personene som svarer på undersøkelsen har noen skjevheter angående produktet undersøkelsen blir gjort for, er resultatet ikke veldig nøyaktig
- Hvis selve utvalget er den rette representanten for befolkningen, vil også i dette tilfellet resultatene være langt unna.
En stor forutsetning her er også at befolkningen normalt er fordelt. Så hvis utvalgsstørrelsen er for liten og populasjonsfordelingen ikke er normal, kan ikke z-poengsum beregnes, og vi vil ikke kunne finne feilmarginen.
Relevans og bruk av formel for margin eller feil
Hver gang vi bruker eksempeldata for å finne noe relevant svar for populasjonssettet, er det en viss usikkerhet og sjanser for at resultatet kan avvike fra det faktiske resultatet. Feilmarginen vil fortelle oss at det som er nivået på avviket er der, er prøven. Vi må minimere feilmarginen slik at prøveresultatene våre viser den faktiske historien om populasjonsdata. Så senk feilmarginen, bedre blir resultatene. Feilmarginen kompletterer og fullfører den statistiske informasjonen vi har. Hvis en undersøkelse for eksempel finner ut at 48% av befolkningen foretrekker å tilbringe tid hjemme i løpet av helgen, kan vi ikke være så presise, og det er noen manglende elementer i den informasjonen. Når vi introduserte en feilmargin her, si 5%, vil resultatet bli tolket som 43-53% mennesker likte ideen om å være hjemme i løpet av helgen, noe som gir full mening.
Marginal of Error Formula Calculator
Du kan bruke følgende feilkalkulator
| Z | |
| S | |
| √n | |
| Feilmargin | |
| Feilmargin | = |
|
|
Anbefalte artikler
Dette har vært en guide til formelen Margin of Error. Her diskuterer vi hvordan du beregner feilmarginen sammen med praktiske eksempler. Vi tilbyr også en margin for feilkalkulator med nedlastbar excel-mal. Du kan også se på følgende artikler for å lære mer -
- Veiledning til formel for rett avskrivning
- Eksempler på Dobling Time Formula
- Hvordan beregne amortisering?
- Formel for sentral begrensningsteorem
- Altman Z Score | Definisjon | eksempler
- Avskrivningsformel | Eksempler med Excel-mal