
Z Score Formula (Innholdsfortegnelse)
- Formel
- eksempler
- Kalkulator
Hva er Z Score Formula?
"Z-poengsum" er et av de mest brukte statistiske verktøyene som brukes til å standardisere poengsum, forutsatt at populasjonsmidler og standardavviket er kjent. Som sådan er Z-poengsum også kjent som standard-poengsummen. Z-poengsum varierer i området -3 ganger standardavviket til +3 ganger standardavviket med et gjennomsnitt på null og et standardavvik på et. Formelen for Z-score for en variabel kan avledes ved å trekke gjennomsnittet av befolkningen fra den gitte variabelen (som er en del av datasettet eller populasjonen) og deretter dele resultatet med standardavviket for befolkningen. Matematisk er det representert som,
Z = (X – μ) / σ
hvor,
- X = Variabel fra befolkningen
- μ = Gjennomsnitt av befolkningen
- σ = Standardavvik for befolkningen
Eksempler på Z-score-formel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av Z-poengsummen på en bedre måte.
Du kan laste ned denne Z Score Formula Excel Template her - Z Score Formula Excel TemplateZ Score Formula - Eksempel # 1
La oss ta eksemplet på Manny som nylig dukket opp for SAT. Han klarte å score 1109 i dette forsøket. I henhold til tilgjengelig informasjon forble imidlertid gjennomsnittlig poengsum for SAT rundt 1030 med et standardavvik på 250. Beregn Z-poengsummen for Mannys SAT-poengsum og vurder hvor godt han gjorde det sammenlignet med de gjennomsnittlige testtakerne.
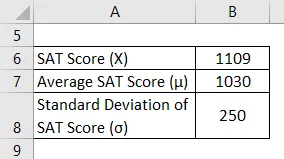
Løsning:
Z-poengsum beregnes ved å bruke formelen nedenfor
Z = (X - μ) / σ
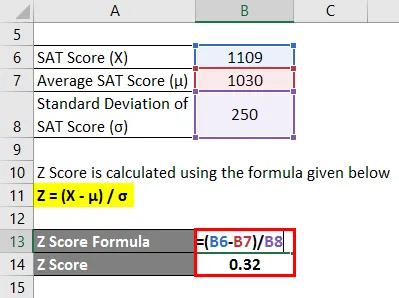
- Z Score = (1109 - 1030) / 250
- Z-score = 0, 32
Derfor er Mannys SAT-score 0, 32 standardavvik høyere enn den gjennomsnittlige testtakernes poengsum, noe som indikerer at 62, 55% av testtakerne scoret mindre enn Manny.
Z Score Formula - Eksempel # 2
La oss ta eksemplet på Chelsea som har skrevet SAT to ganger og vil sammenligne ytelsen sin i dem. Hun klarte å score 1085 og 1059 i henholdsvis 1. og 2. forsøk. I henhold til tilgjengelig informasjon var gjennomsnittlig poengsum og standardavvik under første forsøk henholdsvis 1100 og 230, mens det i sistnevnte var henholdsvis 1050 og 240. Hjelp Chelsea med å bestemme i hvilken eksamen hun presterte bedre.
Løsning:
1. forsøk
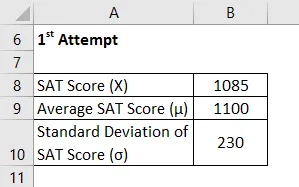
Z-poengsum beregnes ved å bruke formelen nedenfor
Z = (X - μ) / σ
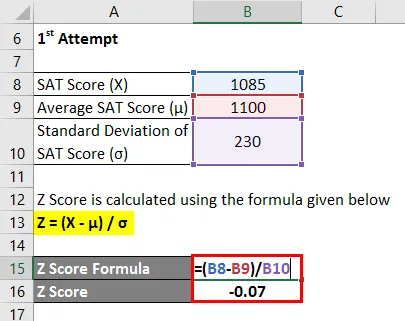
- Z Score = (1085 - 1100) / 230
- Z-score = -0, 07
Derfor er Chelseas SAT-score i 1. forsøk 0, 07 standardavvik lavere enn den gjennomsnittlige testtakernes poengsum, noe som indikerer at 47, 40% av testtakerne scoret mindre enn Chelsea under 1. forsøk.
2. forsøk
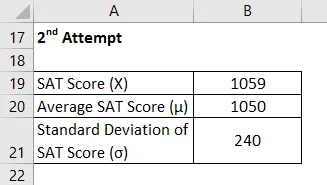
Z-poengsum beregnes ved å bruke formelen nedenfor
Z = (X - μ) / σ
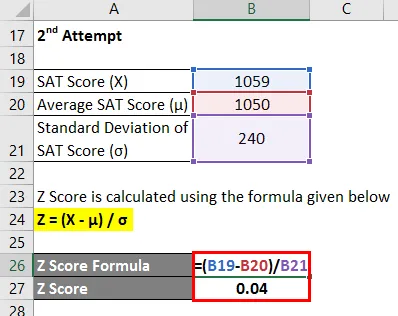
- Z Score = (1059 - 1050) / 240
- Z-poeng = 0, 04
Derfor er Chelseas SAT-poengsum i det andre forsøket 0, 04 standardavvik høyere enn gjennomsnittet av testtakerne, noe som indikerer at 51, 50% av testtakerne scoret mindre enn Chelsea under det 2. forsøket.
Så fra sammenligningen av Z-poengsummene, er det tydelig at Chelsea presterte bedre under sitt 2. forsøk.
Forklaring
Formelen for Z-poengsum kan avledes ved å bruke følgende trinn:
Trinn 1: Bygg først en populasjon med et stort antall variabler, og variablene er betegnet med X i .
Trinn 2: Deretter beregnes antall variabler i befolkningen og betegnes med N.
Trinn 3: Deretter beregnes gjennomsnittet av populasjonen ved å oppsummere alle variablene etterfulgt av divisjon med det totale antall variabler (trinn 2) i datasettet. Gjennomsnittet av befolkningen er angitt med μ.
μ = ∑ X i / N
Trinn 4: Trekk deretter gjennomsnittet fra hver variabel i datasettet for å beregne avviket fra gjennomsnittet.
dvs. (X i - μ) er avviket for det første datapunktet.
Trinn 5: Beregn deretter de kvadratiske avvikene for variablene, dvs. (X i - μ) 2 .
Trinn 6: Legg deretter opp alle de kvadratiske avvikene, og del deretter totalen med antall variabler i datasettet for å komme til variansen.
σ 2 = ∑ (X i - μ) 2 / N
Trinn 7: Deretter blir standardavviket for populasjonen beregnet ved å beregne kvadratroten til variansen beregnet i trinnet ovenfor.
σ = √ ∑ (X i - μ) 2 / N
Trinn 8: Til slutt blir formelen for Z-poengsum avledet ved å trekke gjennomsnittet av befolkningen (trinn 3) fra variabelen og deretter dele resultatet med standardavviket for befolkningen (trinn 7) som vist nedenfor.
Z = (X - μ) / σ
Relevans og bruk av Z Score Formula
Sett fra en statistiker er konseptet Z-poengsum veldig viktig ettersom det er nyttig for å bestemme sannsynligheten for om en hendelse vil skje i en normal fordeling eller ikke. Faktisk brukes Z-poengsum også til å sammenligne to rå score fra to forskjellige normale fordelinger, og det gjøres ved å konvertere rå score til Z-poengsum eller standardisert score. Videre innebærer en positiv Z-score en poengsum som er høyere enn gjennomsnittet, mens en negativ Z-poengsum innebærer en poengsum som er mindre enn gjennomsnittet.
Z Score Formula Calculator
Du kan bruke følgende Z Score Formula Calculator
| X | |
| μ | |
| σ | |
| Z | |
| Z = |
|
|
Anbefalte artikler
Dette har vært en guide til Z Score Formula. Her diskuterer vi hvordan du beregner Z Score sammen med praktiske eksempler. Vi tilbyr også en Z Score-kalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Eksempler på prøvestørrelsesformel
- Hvordan beregne vektet gjennomsnitt?
- Kalkulator for korrelasjonsformel
- Formel for å beregne normal distribusjon
- Eksempler på Altman Z Score