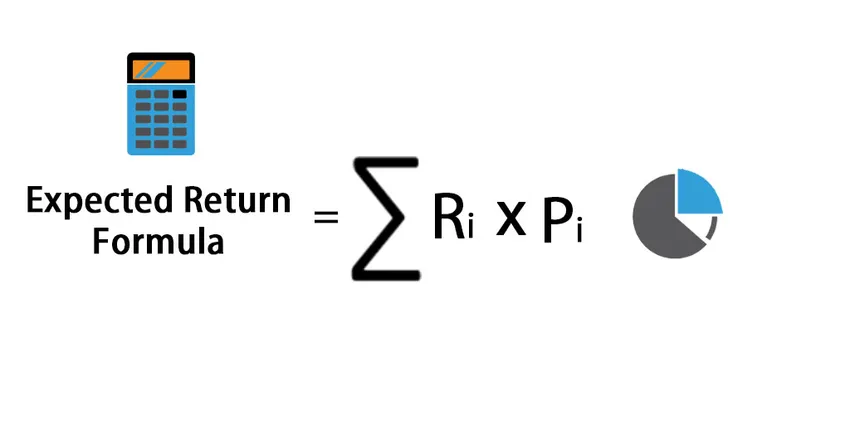
Forventet returformel (innholdsfortegnelse)
- Forventet returformel
- Eksempler på forventet returformel (med Excel-mal)
- Forventet kalkulator for returformulering
Forventet returformel
Forventet avkastning kan defineres som den sannsynlige avkastningen for en portefølje som eies av investorer basert på tidligere avkastning, eller den kan også defineres som en forventet verdi av porteføljen basert på sannsynlighetsfordeling av sannsynlig avkastning.
Her er den forventede returformelen -
Expected Return = Expected Return=∑ (R i * P i )
Hvor
- R i - Return Forventning av hvert scenario
- P i - Sannsynligheten for avkastningen i det scenariet
- i - Mulige scenarier som strekker seg fra 1 til n
Eksempler på forventet returformel (med Excel-mal)
La oss ta et eksempel for å forstå beregningen av forventet returformel på en bedre måte.
Forventet returformel - eksempel # 1
La oss ta et eksempel på en portefølje av aksjer og obligasjoner der aksjer har 50% vekt og obligasjoner har en vekt på 50%. Forventet avkastning på aksjer er 15% og forventet avkastning for obligasjoner er 7%.
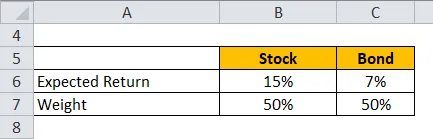
Forventet retur beregnes ved å bruke formelen gitt nedenfor
Forventet avkastning for portefølje = Vekt på aksjen * Forventet avkastning for aksje + Vekt av obligasjonen * Forventet avkastning for obligasjon
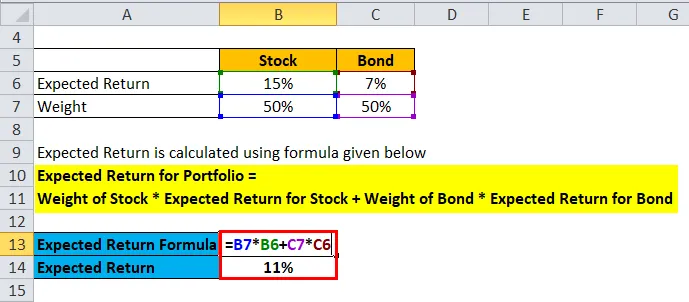
- Forventet avkastning for portefølje = 50% * 15% + 50% * 7%
- Forventet avkastning for portefølje = 7, 5% + 3, 5%
- Forventet avkastning for portefølje = 11%
Forventet returformel - eksempel # 2
La oss ta et eksempel på portefølje som har stock Reliance, Tata Steel, Eicher Motors og ITC.
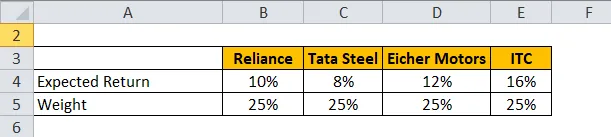
Forventet retur beregnes ved å bruke formelen gitt nedenfor
Forventet avkastning for portefølje = ∑ Vekt på hver aksje * Forventet avkastning for hver aksje

- Forventet avkastning for portefølje = 25% * 10% + 25% * 8% + 25% * 12% + 25% * 16%
- Forventet avkastning for portefølje = 2, 5% + 2% + 3% + 4%
- Forventet avkastning for portefølje = 11, 5%
Forventet returformel - eksempel # 3
La oss ta et eksempel på portefølje av HUL, HDFC og 10 års statsobligasjon.
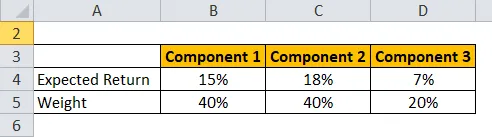
Forventet retur beregnes ved å bruke formelen gitt nedenfor
Forventet avkastning for portefølje = ∑ Vekt på hver komponent * Forventet avkastning for hver komponent
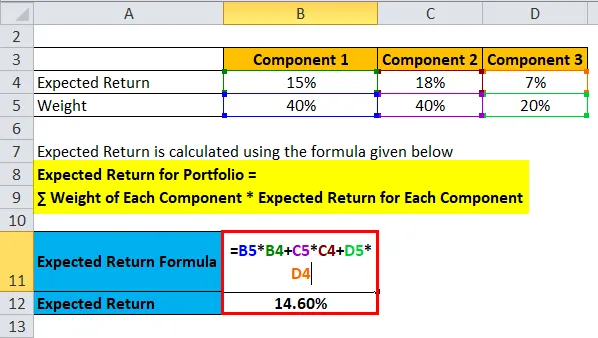
- Forventet avkastning for portefølje = 40% * 15% + 40% * 18% + 20% * 7%
- Forventet avkastning for portefølje = 6% + 7, 2% + 1, 40%
- Forventet avkastning for portefølje = 14, 60%
Du kan laste ned denne Expected Return Formula Excel Template her - Expected Return Formula Excel Template
Forklaring av forventet returformel
Forventet avkastning kan defineres som den sannsynlige avkastningen for en portefølje som eies av investorer basert på tidligere avkastning, eller den kan også defineres som en forventet verdi av porteføljen basert på sannsynlighetsfordeling av sannsynlig avkastning. Den forventede avkastningen kan sees på kort sikt som en tilfeldig variabel som kan ta forskjellige verdier basert på noen forskjellige sannsynligheter. Denne tilfeldige variabelen har verdier innenfor et bestemt område og kan bare ta verdier innenfor det bestemte området. Derfor er den forventede avkastningsberegningen basert på historiske data, og kan derfor ikke være pålitelig når det gjelder å forutse fremtidig avkastning. Det kan sees på som et mål på forskjellige sannsynligheter og sannsynligheten for å få en positiv avkastning på ens investering og verdien av avkastningen.
Hensikten med dette er å gi en investor en ide om for et annet risikonivå hva er de forskjellige scenariene med forskjellige sannsynligheter som vil gi en avkastning som er større enn den risikofrie avkastningen. Som vi alle vet, ville risikofri avkastning være den 10-årige statsobligasjonsrenten til USAs regjering.
Relevans og bruk av forventet returformel
Som nevnt ovenfor er beregnet forventet avkastning basert på historiske data, og har derfor en begrensning av å forutse fremtidig mulig avkastning. Investorer må huske på forskjellige andre faktorer og ikke investere basert på beregnet avkastning. Ta et eksempel: -
Portefølje A - 10%, 12%, -9%, 2%, 25%
Portefølje B - 9%, 7%, 6%, 6%, 12%
Hvis vi vurderer begge de ovennevnte porteføljene, har begge en forventet avkastning på 8%, men portefølje A utviser mye risiko på grunn av mye varians i avkastningen. Derfor må investorer ta hensyn til denne risikoen som beregnes ved tiltak som standardavvik og variasjon.
- Varians - Det kan defineres som en variant av et sett datapunkter rundt deres middelverdi. Det beregnes med det sannsynlighetsvektede gjennomsnittet av kvadrateavvik fra gjennomsnittet. Det er et mål på risiko som investorer må ta hensyn til.
Først må man beregne gjennomsnittet av alle avkastninger. Deretter blir hver avkastes avvik funnet ut fra hovedverdien og kvadratet for å sikre alle positive resultater. Og når de først er kvadratisk multipliseres de med respektive sannsynlighetsverdier for å finne ut avviket.
Porteføljevarians kan beregnes ut fra følgende formel: - Hvis det er to porteføljer A og B
Porteføljevarians = w A 2 * σ A 2 + w B 2 * σ B 2 + 2 * w A * w B * Cov (A, B)
Hvor Cov (A, B) - er samvariasjon av porteføljer A og B
- Standardavvik - Det er et annet mål som angir avviket fra dets gjennomsnitt. Standardavvik beregnes ved å ta en firkantet rot av varians og betegnes med σ.
Forventet kalkulator for returformulering
Du kan bruke følgende kalkulator for forventet retur.
| R 1 | |
| P 1 | |
| R 2 | |
| S 2 | |
| R 3 | |
| S 3 | |
| R 4 | |
| S 4 | |
| Forventet tilbakekomst | |
| Forventet retur = | R 1 * P 1 + R 2 * P 2 + R 3 * P 3 + R 4 * P 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Konklusjon
Forventet avkastning kan defineres som den sannsynlige avkastningen for en portefølje som eies av investorer basert på tidligere avkastning. Siden det bare benytter tidligere avkastning, er det derfor en begrensning, og verdien av forventet avkastning bør ikke være en eneste faktor som investorer vurderer når de bestemmer om de vil investere i en portefølje eller ikke. Det er andre tiltak som må sees på, for eksempel porteføljens varians og standardavvik.
Anbefalte artikler
Dette har vært en guide til forventet returformel. Her diskuterer vi Hvordan beregne forventet avkastning sammen med praktiske eksempler. Vi tilbyr også Expected Return Calculator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Veiledning for formel for omsetningsgrad
- Guide to Bid Ask Spread Formula
- Hvordan beregne kapasitetsutnyttelsesgrad?
- Beregning av obligasjonsekvivalent avkastning
- Omsetningsforholdsformel | Eksempler | Excel-mal