Vektet gjennomsnittlig formel (innholdsfortegnelse)
- Vektet gjennomsnittlig formel
- Vektet gjennomsnittlig kalkulator
- Vektet gjennomsnittlig formel i Excel (med Excel-mal)
Vektet gjennomsnittlig formel
Formelen for beregning av vektet gjennomsnitt er som følger:
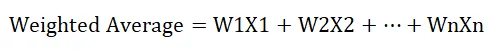
Hvor,
- W angir relativ vekt (i%)
- X betegner verdi
Eksempler på vektet gjennomsnittlig formel
La oss se noen eksempler for å forstå vektet gjennomsnittlig formel:
Eksempel 1
La oss anta at Anand har investert pengene i følgende forholdsmessige: 40% i investering A, 20% i investering B og 40% i investering C. Disse investeringene har en avkastningssats som følger: Investering A som 15%, investering B som 10 %, og investering C som henholdsvis 20%. Vi må beregne et vektet gjennomsnitt for avkastningssatsene Anand ville motta.
Her,
- Vi har relative vekter for investeringene A, B & C som henholdsvis 40%, 20% og 40%.
- Og verdi (avkastning) for investeringene A, B & C som henholdsvis 15%, 10% og 20%.
Ved å bruke den vektede gjennomsnittsformelen, får vi-
- Vektet gjennomsnitt = W1 X1 + W2 X2 + …… + Wn Xn
- Vektet gjennomsnitt = 40% * 15% + 20% * 10% + 40% * 20%
- Vektet gjennomsnitt = 16%
Dette viser at Anand vil motta 16% vektingsgjennomsnittlig avkastning fra Investeringer A, B & C.
Eksempel 2
La oss anta at Anand har meldt seg på et matematikkurs, den endelige karakteren hans vil bli bestemt ut fra følgende kategorier: tester 30%, avsluttende eksamen 40%, quizer 15% og lekser 15%.
Anand har scoret følgende karakter i hver kategori: Tester-80, avsluttende eksamen-65, quizer-85, lekser-90. Nå må vi finne ut karakteren til Anand.
For å beregne et vektet gjennomsnitt med prosenter, må hver kategoriverdi ganges med prosenten. Da må alle disse nye verdiene legges sammen.
Her,
Vi har relative vekter for følgende kategorier som følger:
- Tester 30%
- Avsluttende eksamen 40%
- quizer 15%
- lekser 15%
Og verdi (merker) for kategoriene som
- Tester-80
- Avsluttende eksamen-65,
- quiz-85
- lekser-90
Ved å bruke den vektede gjennomsnittsformelen, får vi-
- Vektet gjennomsnitt = W1 X1 + W2 X2 + …… + WnXn
- Vektet gjennomsnitt = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
- Vektet gjennomsnitt = 76, 25 eller 76%
Dette viser den totale karakteren til Anand er 76%.
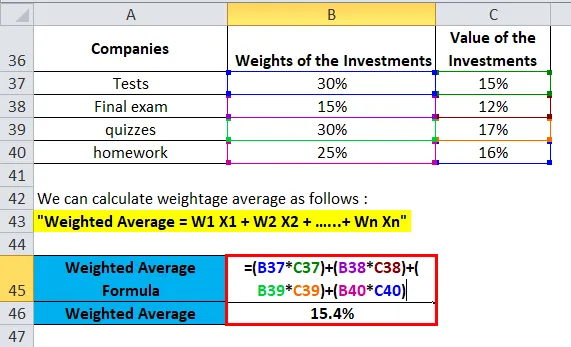
Eksempel 3
La oss anta at Jagriti har investert penger i aksjer i forskjellige selskaper. Jagriti-porteføljen består av 30% i A, 15% i A, B, 30% i A C og de resterende 25% i A. Forventet avkastning i henhold til dagens markedssituasjon på disse Aksjene er som følger: Avkastning på A er 15%, avkastning på lager B er 12%, avkastning på lager C er 17% og avkastning på lager D er henholdsvis 16%. Jagriti ønsker å beregne sitt gjennomsnittlige avkastning på porteføljen i henhold til dagens markedssituasjon.
Her,
- Vi har relative vekter av aksjene i porteføljen som følger: A, B, C & D som henholdsvis 30%, 15%, 30% og 25%.
- Og verdi (Return Rate) for aksjene som følger: A, B, C & D som henholdsvis 15%, 12%, 17% og 16%.
Ved å bruke den vektede gjennomsnittsformelen, får vi-
- Vektet gjennomsnitt = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
- Vektet gjennomsnitt = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
- Vektet gjennomsnitt = 0, 154 eller 15, 4%
Dette viser at Jagriti vil motta 15, 4% vektavkastning fra porteføljen av aksjer A, B, C og D.
Forklaring av vektet gjennomsnittlig formel
Vektet gjennomsnittlig formel brukes for å beregne gjennomsnittsverdien for et bestemt sett med tall med forskjellige nivåer av relevans. Vektene må være representert med tanke på total relevans i prosent. Vektene som er tatt, skal være lik 100%, eller 1.
For å beregne vektet gjennomsnittlig formel, trenger vi relativ vekt og verdi.
Den første komponenten er relativ vekt og den andre komponenten er verdiinnganger. For å beregne vektet gjennomsnitt må vi ha spesifikk vekt for hver variabel tatt som verdi, og vektingen må være lik 100%.
Betydning og bruk av vektet gjennomsnittlig formel
Det vektede gjennomsnittet brukes i forskjellige økonomiske formler. Få eksempler på Vektet gjennomsnittlig beta og en vektet gjennomsnittlig kapitalkostnad (WACC).
Vi er kjent med ideen om å finne det athematiske middelverdien eller gjennomsnittet for en serie varer. Vi kan ganske enkelt legge opp verdier for alle elementene og dele dem med det totale antall elementer for beregning av gjennomsnittet. Dette fungerer bare hvis alle elementene er vektet likt. For å beregne de gjennomsnittlige månedlige mobilregningene for et år, kan vi for eksempel ganske enkelt legge opp de totale fakturerte beløpene de siste tolv månedene og dele dem med tolv, så kan vi få en grov idé om den gjennomsnittlige fakturaen som er betalt, siden mobilen regningssyklus er omtrent for samme tidsperiode, dvs. en måned.
La oss si at du vil beregne gjeldende gjennomsnittlig kursklasse i matematikklassen din. Vanligvis tillegger de fleste klassene annen vekt til eksamen enn til lekseroppgaver, intern test og konkurranser. I dette tilfellet må du beregne et vektet gjennomsnitt, som tar den spesifikke vekten til hvert emne for å beregne kursklassen din.
Eksempel på noen få tilfeller hvor du må bruke et vektet gjennomsnitt i stedet for et enkelt gjennomsnitt. Første tilfelle - Når vi ønsker å beregne et gjennomsnitt som har forskjellige prosentverdier for forskjellige kategorier. Eksemplet ovenfor på kurset er de samme tilfellene. Og for det andre når vi har en stor gruppe varer med en annen regelmessighet.
Hvis et selskap har en stor svingning i salget på grunn av produksjonen av et sesongprodukt, kan de bruke den vektede gjennomsnittlige formelen. Og selskapet ønsker å beregne gjennomsnittet for de variable utgiftene sine, da kan selskapet bruke den vektede gjennomsnittlige formelen og ta salget som vekt for å få en bedre forståelse av utgiftene deres. Og kan sammenligne mengden de produserer eller selger.
Vektet gjennomsnittlig kalkulator
Du kan bruke den følgende vektede kalkulatoren
| W 1 | |
| X 1 | |
| W 2 | |
| X 2 | |
| W 3 | |
| X 3 | |
| W 4 | |
| X 4 | |
| Vektet gjennomsnittlig formel | |
| Vektet gjennomsnittlig formel = | W 1 * X 1 + W 2 * X 2 + W 3 * X 3 + W 4 * X 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Vektet gjennomsnittlig formel i Excel (med Excel-mal)
Her vil vi gjøre det samme eksemplet på vektet gjennomsnittformel i Excel. Det er veldig enkelt og enkelt. Du må oppgi de to inngangene, dvs. relative vekter og avkastningshastighet.
Du kan enkelt beregne det vektede gjennomsnittet ved å bruke formel i malen som følger med.
vektingsgjennomsnittlig avkastning fra investeringene A, B & C beregnes som:

total karakter av Anand beregnes som:

vekt Aldersgjennomsnitt avkastning fra porteføljen av aksjer A, B, C og D er beregnet som:
Du kan laste ned denne vektet gjennomsnittlig formel Excel-mal her - vektet gjennomsnittlig formel Excel-mal
Anbefalte artikler
Dette har vært en guide til en vektet gjennomsnittformel. Her diskuterer vi bruksområdene sammen med praktiske eksempler. Vi gir deg også en vektet gjennomsnittlig kalkulator med nedlastbar Excel-mal. Du kan også se på følgende artikler for å lære mer -
- Hvordan beregne overhead ratio?
- Beregn egenkapitalmultiplikator med eksempler
- Bruk av bruttomarginalformel
- Veiledning for omregning av kundefordringer